| Codeforces Round 421 (Div. 2) |
|---|
| Закончено |
Однажды, разбираясь в своих каждодневных заботах, Мистеру Б понадобилось получить угол a и начертить его на своем поле. Так случилось, что инопланетяне оставили уже множество различных фигур на его поле, среди которых был правильный n-угольник (правильный многоугольник с n сторонами).
Именно этой фигурой Мистер Б и решил воспользоваться. Теперь Мистеру Б необходимо найти три попарно различные вершины многоугольника v1, v2, v3 такие, что угол 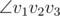 (т.е. угол, в котором v2 — вершина, а v1 и v3 лежат на сторонах) будет как можно ближе к a. Иными словами, необходимо, чтобы величина
(т.е. угол, в котором v2 — вершина, а v1 и v3 лежат на сторонах) будет как можно ближе к a. Иными словами, необходимо, чтобы величина 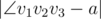 — была минимально возможной.
— была минимально возможной.
При этом Мистера Б устроит любое из возможных решений.
В первой и единственной строке через пробел заданы два целых числа: n и a (3 ≤ n ≤ 105, 1 ≤ a ≤ 180) — количество вершин в многоугольнике и необходимый угол в градусах.
Выведите через пробел три различные вершины многоугольника v1, v2, v3, образующие угол 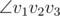 . Если существует несколько решений, выведите любое. Вершины многоугольника нумеруются от 1 до n в порядке обхода по часовой стрелке.
. Если существует несколько решений, выведите любое. Вершины многоугольника нумеруются от 1 до n в порядке обхода по часовой стрелке.
3 15
1 2 3
4 67
2 1 3
4 68
4 1 2
В первом примере вершины равностороннего треугольника могут давать только угол в 60 градусов, поэтому ответом является любой возможный угол.
В квадрате же можно получить только углы в 45 и 90 градусов. Поэтому во втором примере выбирается угол в 45 градусов, так как |45 - 67| < |90 - 67|. Корректными также являются ответы: "3 1 2", "3 2 4", "4 2 3", "4 3 1", "1 3 4", "1 4 2", "2 4 1", "4 1 3", "3 1 4", "3 4 2", "2 4 3", "2 3 1", "1 3 2", "1 2 4", "4 2 1".
В третьем примере, напротив, выбирается угол в 90 градусов, так как |90 - 68| < |45 - 68|. Корректными также являются ответы: "2 1 4", "3 2 1", "1 2 3", "4 3 2", "2 3 4", "1 4 3", "3 4 1".
| Название |
|---|




