| Codeforces Round 408 (Div. 2) |
|---|
| Закончено |
Однажды у Зейна была хорошая последовательность a из n целых чисел a1, a2, ..., an, но он ее потерял.
Последовательность называется хорошей, если и только если все ее элементы — целые неотрицательные числа, не превосходящие 109.
Однако, Зейн помнит, что он играл с последовательностью, применяя к ней m операций.
Было два типа операций:
1. Найти максимальное значение среди чисел с индексами i такими, что l ≤ i ≤ r, по данным l и r.
2. Присвоить значение d элементу последовательности с индексом k, по данным k и d.
После того, как он поиграл с последовательностью, он восстановил массив до исходного состояния. Это значит, что пропали изменения в последовательности a, внесенные операциями типа 2. После этого Зейн потерял последовательность.
К счастью, Зейн помнит все операции, их порядок, а также результат всех операций типа 1, которые оказались различными. Кроме этого, Зейн знает, что среди всех хороших последовательностей, которые произвели бы те же результаты после применения этих операций в соответствующем порядке, последовательность a имела наибольшую красоту.
Красота последовательности — это побитовый OR всех элементов последовательности. Например, красота последовательности Зейна a равняется a1 OR a2 OR ... OR an.
Зейн понимает, что не всегда возможно точно восстановить потерянную последовательность по данной информации, поэтому он будет доволен получить любую хорошую последовательность b, состоящую из n целых чисел b1, b2, ..., bn такую, что:
1. она даст такой же результат при применении данных операций;
2. имеет такую же красоту, как и последовательность Зейна a.
Если такая последовательность существует, найдите ее. Иначе сообщите, что Зейн запомнил что-то неправильно.
Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 3·105) — число элементов в последовательности Зейна и число операций, соответственно.
Строка i из следующих m строк начинается с одного целого числа ti (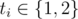
) — типа i-й операции.
Если операция типа 1 (ti = 1), то далее три числа li, ri и xi следуют (1 ≤ li ≤ ri ≤ n, 0 ≤ xi ≤ 109) — параметры операции и максимальный элемент среди элементов с индексами от li до ri, включительно.
Если операция типа 2 (ti = 2), то далее следуют два целых числа ki и di (1 ≤ ki ≤ n, 0 ≤ di ≤ 109), что означает, что элемент с индексом ki должен стать равным di после этой операции.
Гарантируется, что xi ≠ xj для всех пар (i, j) таких, что 1 ≤ i < j ≤ m, и ti = tj = 1.
Операции даны в том порядке, в котором они применялись. То есть, первой дана операция, которая применялась первой, и так далее.
Если не существует подходящей хорошей последовательности, выведите «NO» (без кавычек) в единственной строке.
Иначе, выведите «YES» (без кавычек) на первой строке, и n целых чисел b1, b2, ..., bn (0 ≤ bi ≤ 109) на второй строке.
Если существует несколько ответов, выведите любой из них.
5 4
1 1 5 19
1 2 5 1
2 5 100
1 1 5 100
YES
19 0 0 0 1
5 2
1 1 5 0
1 1 5 100
NO
В первом примере легко показать, что данная хорошая последовательность подходит. В частности, ее красота равна 19 OR 0 OR 0 OR 0 OR 1 = 19.
Во втором примере ясно, что две операции противоречат друг другу, поэтому не существует подходящей хорошей последовательности.
