Два друга Аксель и Марстон вместе путешествуют по Битландии. В Битландии n городов, некоторые пары из которых соединены однонаправленными дорогами. Дороги в Битландии бывают пешеходные и велосипедные. В Битландии может быть несколько дорог между каждой парой городов, и бывают даже дороги из города в него же. Однако, никакие две дороги в Битландии не могут иметь одинаковые начало, конец и тип одновременно.
Друзья находятся в городе 1 и хотят составить маршрут путешествия. Аксель любит ходить пешком, а Марстон предпочитает велосипед. Чтобы маршрут получился разнообразным и интересным для каждого из друзей, они выбирают порядок чередования типов пройденных дорог следующим образом:
- Маршрут начинается с пешеходной дороги.
- Пусть известное начало маршрута записано в виде строки s из букв П (пешеходная дорога) и В (велосипедная дорога). Тогда к маршруту s дописывается строка
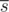 , где
, где 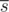 означает строку s, в которой тип каждой дороги заменен на противоположный (все пешеходные дороги на велосипедные, и наоборот).
означает строку s, в которой тип каждой дороги заменен на противоположный (все пешеходные дороги на велосипедные, и наоборот).
Первые несколько шагов построения маршрута будут выглядеть так: П, ПВ, ПВВП, ПВВПВППВ, ПВВПВППВВППВПВВП, и так далее.
Далее, друзья начинают движение в городе 1 по дорогам Битландии, каждый раз выбирая тип очередной дороги в соответствии с очередным символом маршрута. Если же подходящую дорогу выбрать не удается, друзья заканчивают свое путешествие и летят домой.
Помогите друзьям определить максимально возможную продолжительность своего путешествия, если они будут следовать построенной последовательности типов дорог. Если друзья могут найти путь, состоящий более, чем из 1018 дорог, вместо длины выведите -1.
Первая строка содержит два целых числа n и m (1 ≤ n ≤ 500, 0 ≤ m ≤ 2n2) — количество городов и дорог в Битландии соответственно.
Следующие m строк описывают дороги. В i-ой из этих строк записано три целых числа vi, ui и ti (1 ≤ vi, ui ≤ n, 0 ≤ ti ≤ 1), где vi и ui — номера городов, являющихся началом и концом i-ой дороги, а ti задает тип i-ой дороги (0 — пешеходная дорога, 1 — велосипедная дорога). Гарантируется, что для каждой пары различных чисел i, j, таких что 1 ≤ i, j ≤ m, либо vi ≠ vj, либо ui ≠ uj, либо ti ≠ tj.
Если друзья могут найти подходящий путь длины строго большей, чем 1018, выведите одно число -1. В противном случае выведите максимальную длину подходящего пути, то есть наибольшее количество дорог, которое могут пройти друзья.
2 2
1 2 0
2 2 1
3
2 3
1 2 0
2 2 1
2 2 0
-1
В первом примере путь длины 3 можно получить, пройдя один раз по дороге 1 из города 1 в город 2, после чего дважды по дороге 2 из города 2 в него же.
Во втором примере мы можем получить путь сколь угодно большой длины, сперва пройдя по дороге 1, а после этого выбирая дорогу 2 или 3 в зависимости от очередного типа дороги.
| Название |
|---|




