| VK Cup 2017 - Раунд 1 |
|---|
| Закончено |
Мишляндия имеет форму большого квадрата на плоскости. Страна состоит из всех точек с координатами, по модулю не превосходящими 106.
Всего в Мишляндии n домов. Дом номер i расположен в точке (xi, yi). Все эти n точек различны, однако, некоторые подмножества этих точек могут лежать на одной прямой.
Мишка Лимак живет в первом доме. Он хочет снести свой дом и построить новый в какой-нибудь точке Мишляндии.
Медведи не любят больших перемен. Поэтому после того, как Лимак перенесет свой дом, для каждой тройки домов, расположенных в точках pi, pj и pk, знак псевдовекторного произведения (pj - pi) × (pk - pi) должен остаться таким же, каким он был до переселения Лимака. Иными словами, если знак был отрицательным/положительным/нулем, то он должен остаться отрицательным/положительным/нулем соответственно. Это условие должно быть выполнено для всех троек индексов (i, j, k), в том числе равных друг другу, а также отличных от 1. Кроме того, Лимак не может построить дом в точке, где находится дом другого медведя (однако, можно построить дом там же, где был старый дом).
Разность и псевдовекторное произведение точек (ax, ay) и (bx, by) мы определяем следующим образом:
Рассмотрим множество точек, в которых Лимак может построить новый дом. Ваша задача — найти площадь этого множества.
Формально, пусть Лимак выбирает расположение нового дома случайным образом внутри страны (т. е. каждая из координат выбирается независимо равновероятно из отрезка [ - 106, 106]). Пусть p — вероятность того, что выбранное расположение нового дома допустимо. Пусть S — площадь Мишляндии (S = 4·1012). Вам необходимо найти p·S.
В первой строке находится одно целое число T (1 ≤ T ≤ 500) — количество тестовых случаев. Далее следуют описания тестовых случаев.
Первая строка описания тестового случая содержит одно целое число n (3 ≤ n ≤ 200 000) — количество домов.
Строка i из следующих n строк содержит два целых числа xi и yi ( - 106 ≤ xi, yi ≤ 106) — координаты i-го дома. Никакие два дома в одном тестовом случае не находятся в одной точке. Лимак живет в первом доме.
Сумма величин n не превосходит 200 000.
Выведите одно вещественное число — площадь множества точек, в которых Лимак может построить новый дом.
Ответ будет считаться правильным, если его абсолютная или относительная погрешность не превосходит 10 - 6. Формально, если ответ жюри b, а ваш ответ a, он будет считаться правильным, если 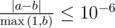 .
.
4
4
5 3
0 1
10 1
3 51
3
-999123 700000
-950000 123456
-950000 987654
3
2 3
10 -1
-4 6
5
1 3
5 2
6 1
4 4
-3 3
250.000000000000
100000000000.000000000000
0.000000000000
6.562500000000
В примере 4 тестовых случая.
В первом тестовом случае всего в Мишляндии четыре дома. Дом Лимака расположен в точке (5, 3). Множество корректных точек для нового расположения точек — треугольник с вершинами в точках (0, 1), (10, 1) и (3, 51). Стороны и вершины треугольника не входят во множество. Площадь этого прямоугольника равна 250.
Во втором тестовом случае множество точек, в которых Лимак может построить дома, образует прямоугольник ширины 50 000 и высоты 2 000 000. Не забудьте, что новое расположение дома должно принадлежать Мишляндии.
В третьем тестовом случае все три точки лежат на одной прямой. Все псевдовекторные произведения равны 0, и должны остаться равными 0 после смены расположения дома. Поэтому Лимак должен построить свой дом на прямой, проходящей через данные три точки. Кроме того, новая позиция дома должна принадлежать квадрату Мишляндии, поэтому множество корректных расположений представляет собой отрезок (кроме двух точек, где уже находятся другие дома). Площадь любого отрезка равна 0.
| Название |
|---|




