| Codeforces Round 396 (Div. 2) |
|---|
| Закончено |
Махмуд и Ехаб живут в стране, в которой n городов, пронумерованных от 1 до n, соединенных n - 1 двунаправленными дорогами. Гарантируется, что из любого города можно добраться в любой другой используя только эти дороги. Про каждый город известна некоторая величина ai.
Определим расстояние от города x до города y как xor чисел, известных про города на пути от x до y (включая как x, так и y). Другими словами, если мы выпишем все величины городов на пути от x до y в массив p длины l, то расстояние между ними будет равно  , где
, где  — операция побитовый xor.
— операция побитовый xor.
Махмуд и Ехаб хотят выбрать два города и проехать от одного до другого. Номер города, в котором они стартуют, всегда не больше номера города, в котором они финишируют (они могут стартовать и закончить в одном и том же городе, тогда расстояние будет равно величине, известной про этот город). Они никак не могут выбрать эти два города, поэтому они попробуют каждый город как старт и каждый город с не меньшим индексом как финиш. Определите суммарное расстояние между всеми этими парами городов.
В первой строке находится целое число n (1 ≤ n ≤ 105) — число городов в стране Махмуда и Ехаба.
Вторая строка содержит n целых чисел a1, a2, ..., an (0 ≤ ai ≤ 106), которые описывают величины, известные про города. Величина ai известна про город i.
Каждая из следующих n - 1 строк содержит два числа u и v (1 ≤ u, v ≤ n, u ≠ v), означающие, что между городами u и v существует двунаправленная дорога. Гарантируется, что можно доехать от любого города до любого другого по данным дорогам.
Выведите одно число — суммарное расстояние между всеми возможными парами городов.
3
1 2 3
1 2
2 3
10
5
1 2 3 4 5
1 2
2 3
3 4
3 5
52
5
10 9 8 7 6
1 2
2 3
3 4
3 5
131
Операция побитовый xor принимает два целых битовых числа одинаковой длины и выполняет логическую операцию xor на каждой паре соответсвующих бит. Результат в позиции равен 1, если и только если только первый бит 1 или только второй бит 1, и результат равен 0 если оба бита 0 или оба бита 1. Больше информации о побитовом xor можно найти здесь: https://ru.wikipedia.org/wiki/Битовые_операции#.D0.98.D1.81.D0.BA.D0.BB.D1.8E.D1.87.D0.B0.D1.8E.D1.89.D0.B5.D0.B5_.D0.98.D0.9B.D0.98_.28XOR.29.
В первом тесте из примера возможные пути следующие:
- из города 1 в него самого, расстояние 1,
- из города 2 в него самого, расстояние 2,
- из города 3 в него самого, расстояние 3,
- из города 1 в город 2, расстояние
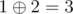 ,
, - из города 1 в город 3, расстояние
 ,
, - из города 2 в город 3, расстояние
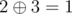 .
.
| Название |
|---|




