Ваня хочет уменьшить дерево. Для этого он может произвольное количество раз выполнять следующую операцию. Сначала Ваня выбирает вершину v и два пути одной длины, идущих из неё и не имеющих никаких общих вершин, кроме v. Обозначим эти пути за a0 = v, a1, ..., ak и b0 = v, b1, ..., bk. Кроме того, у вершин a1, ..., ak, b1, ..., bk не должно быть других соседей, кроме соседних вершин в соответствующем пути. После этого Ваня может «наложить» один путь на другой, тем самым, фактически, удалив вершины b1, ..., bk:
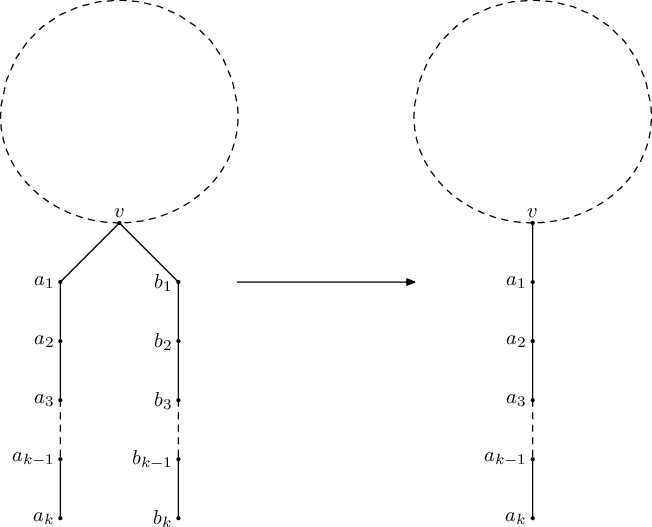
Помогите Ване определить, можно ли последовательным применением этой операции получить из дерева путь. Если ответ положительный, также определите минимально возможную длину такого пути.
Первая строка входного файла содержит единственное целое число n — количество вершин в дереве (2 ≤ n ≤ 2·105).
Следующие n - 1 строк описывают рёбра дерева. Каждая из этих строк содержит два целых числа u и v (1 ≤ u, v ≤ n, u ≠ v), разделённых пробелом: номера концов соответствующего ребра. Гарантируется, что заданный граф является деревом.
Если получить путь невозможно, выведите -1. Иначе выведите минимально возможное число ребер в пути.
6
1 2
2 3
2 4
4 5
1 6
3
7
1 2
1 3
3 4
1 5
5 6
6 7
-1
В первом примере можно получить путь из трех ребер после наложения путей 2 - 1 - 6 и 2 - 4 - 5.
Во втором примере нельзя совершить ни одной корректной операции. Например, нельзя склеить пути 1 - 3 - 4 и 1 - 5 - 6, поскольку у вершины 6 есть сосед 7, которого нет в соответствующем пути.
| Название |
|---|




