У Артема есть друг Сандерс из университета Чикаго. Сандерс предложил Артему следующую задачу.
Обозначим за [n] множество {1, ..., n}. Также мы будем использовать обозначение f: [x] → [y], чтобы показать, что функция f имеет значения в точках 1, ..., x, и все эти значения — целые числа от 1 до y.
Итак, вам дана функция f: [n] → [n]. Ваша задача в том, чтобы найти целое положительное число m и две функции g: [n] → [m], h: [m] → [n], такие что g(h(x)) = x для всех 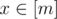 и h(g(x)) = f(x) для всех
и h(g(x)) = f(x) для всех  , либо определите, что найти их невозможно.
, либо определите, что найти их невозможно.
В первой строке входного файла содержится целое число n (1 ≤ n ≤ 105).
Во второй строке содержатся n целых чисел, разделённых пробелами — значения f(1), ..., f(n) (1 ≤ f(i) ≤ n).
Если найти требуемые функции невозможно, выведите -1.
Иначе, на первой строке выведите число m (1 ≤ m ≤ 106). На второй строке выведите n чисел g(1), ..., g(n). На третьей строке выведите m чисел h(1), ..., h(m).
Если существует несколько верных ответов, вы можете вывести любой из них. Гарантируется, что если ответ существует, то также существует ответ, подходящий под указанные ограничения.
3
1 2 3
3
1 2 3
1 2 3
3
2 2 2
1
1 1 1
2
2
2 1
-1
| Название |
|---|




