| Codeforces Round 392 (Div. 2) |
|---|
| Закончено |
Для заданных n, l и r найдите количество различных геометрических прогрессий, каждая из которых состоит из n различных целых чисел не меньших l и не больших r. Иными словами, для каждой прогрессии должно выполняться: l ≤ ai ≤ r и ai ≠ aj , где a1, a2, ..., an —геометрическая прогрессия, 1 ≤ i, j ≤ n и i ≠ j.
Геометрическая прогрессия — последовательность чисел a1, a2, ..., an, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое, не равное нулю, число d — знаменатель прогрессии. Заметим что в рамках нашей задачи d может быть не целым, например в прогрессии 4, 6, 9, знаменатель прогрессии 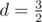 .
.
Две прогрессии a1, a2, ..., an и b1, b2, ..., bn различны, если найдётся такое i (1 ≤ i ≤ n), что ai ≠ bi.
Первая и единственная строка содержит три целых числа n, l и r (1 ≤ n ≤ 107, 1 ≤ l ≤ r ≤ 107).
Выведите одно целое число K — ответ на задачу.
1 1 10
10
2 6 9
12
3 1 10
8
3 3 10
2
Возможные прогрессии для первого теста из примеров:
- 1;
- 2;
- 3;
- 4;
- 5;
- 6;
- 7;
- 8;
- 9;
- 10.
Возможные прогрессии для второго теста из примеров:
- 6, 7;
- 6, 8;
- 6, 9;
- 7, 6;
- 7, 8;
- 7, 9;
- 8, 6;
- 8, 7;
- 8, 9;
- 9, 6;
- 9, 7;
- 9, 8.
Возможные прогрессии для третьего теста из примеров:
- 1, 2, 4;
- 1, 3, 9;
- 2, 4, 8;
- 4, 2, 1;
- 4, 6, 9;
- 8, 4, 2;
- 9, 3, 1;
- 9, 6, 4.
Возможные прогрессии для четвёртого теста из примеров:
- 4, 6, 9;
- 9, 6, 4.
| Название |
|---|




