Баш решил сделать перерыв в своем пути к становлению величайшим мастером покемонов, и поиграть с функциями.
Баш определил функцию f0(n), которая равна числу способов разложить число n на два множителя p и q такие, что gcd(p, q) = 1. Другими словами, f0(n) — число упорядоченных пар натуральных чисел (p, q) таких, что p·q = n и gcd(p, q) = 1.
Но Баш почувствовал, что эту функцию слишком просто посчитать. Поэтому он определил набор функций, где fr + 1 определена как:
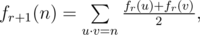
где (u, v) — упорядоченная пара натуральных чисел, при этом они не обязательно взаимно простые.
Теперь Баш хочет узнать некоторые значения fr(n) для различных r и n. Так как эти значения могут быть большими, он хочет узнать остаток от деления этих значений на 109 + 7. Помогите ему!
Первая строка содержит целое число q (1 ≤ q ≤ 106) — число значений, которые хочет знать Баш.
Каждая из следующих q строк содержит два целых числа r и n (0 ≤ r ≤ 106, 1 ≤ n ≤ 106), что значит, что Баш хочет знать значение fr(n).
Выведите q чисел. Для каждой данной пары r и n выведите остаток от деления fr(n) на 109 + 7 на отдельной строке.
5
0 30
1 25
3 65
2 5
4 48
8
5
25
4
630
| Название |
|---|




