| Good Bye 2016 |
|---|
| Закончено |
Одной из популярных традиций встречи нового года является запуск в небо фейерверков. Обычно фейерверк взлетает вертикально вверх в течение некоторого времени, после чего взрывается и разделяется на несколько частей, летящих в разных направлениях. Иногда эти части через некоторое время снова взрываются, также разделяясь на несколько частей и так далее.
Лимак живёт на бесконечном клетчатом поле и у него есть один фейерверк. Поведение этого фейерверка после запуска описывается рекурсией глубины n и продолжительностью каждого из уровней рекурсии t1, t2, ..., tn. Как только Лимак запустит фейерверк в какой-нибудь клетке поля, тот начнёт двигаться вверх. После прохождения t1 клеток (включая стартовую) он взрывается и разделяется на две части, каждая из которых двигается в направлении, изменённом на 45 градусов (для лучшего понимания посмотрите картинки ниже). Таким образом, одна часть будет двигаться в направлении вверх и влево, а другая в направлении вверх и вправо. Каждая из этих частей пройдёт t2 клеток, после чего также разделится на две части, каждая из которых также изменит траекторию на 45 градусов. Процесс будет продолжаться до n-го уровня рекурсии, после чего все 2n - 1 частей взорвутся и исчезнут не создавая новых частей.
После нескольких уровней рекурсивного разделения частей фейерверка может так оказаться, что две или более частей находятся в одной и той же клетке в один и тот же момент времени — такая ситуация разрешена и эти части не сталкиваются.
Перед тем как запустить данный фейерверк Лимак хочет убедиться в безопасности этого запуска. Сможете ли вы посчитать количество клеток, которые хотя бы один раз будут посещены какой-либо частью фейерверка?
В первой строке входных данных записано целое число n (1 ≤ n ≤ 30) — глубина рекурсии разделения фейерверка на части.
Во второй строке записаны n целых чисел t1, t2, ..., tn (1 ≤ ti ≤ 5). На i-м уровне каждая из 2i - 1 частей фейерверка пройдёт ti клеток перед тем как взорвётся.
Выведите одно целое число, равное количеству клеток которые будут посещены хотя бы одной частью фейерверка хотя бы один раз.
4
4 2 2 3
39
6
1 1 1 1 1 3
85
1
3
3
Рассмотрим первый пример. Рисунки ниже показывают как будет выглядеть процесс работы фейерверка после каждого уровня рекурсии. Лимак запускает фейерверк из самой нижней красной клетки. После прохождения t1 = 4 клеток (отмеченных красным) он взрывается и делится на две части (их дальнейшее движение показано зелёным). Все взрывы отмечены символом «X». На последнем рисунке присутствуют 4 красных, 4 зелёных, 8 оранжевых и 23 розовых клетки. Таким образом, итоговое количество посещённых клеток равняется 4 + 4 + 8 + 23 = 39.
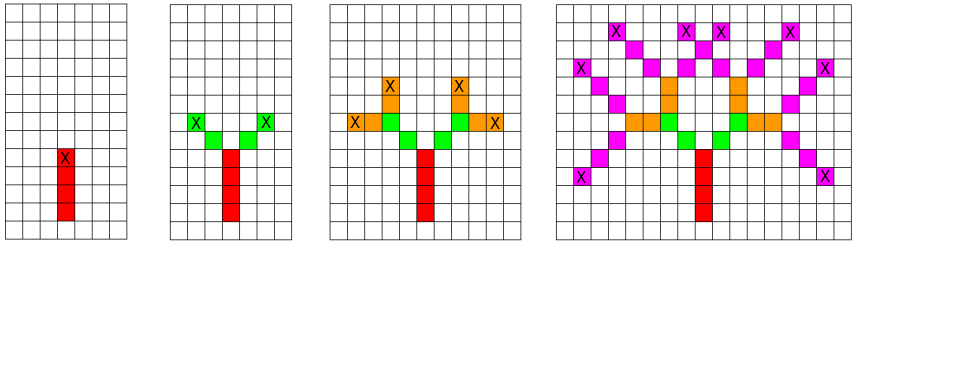
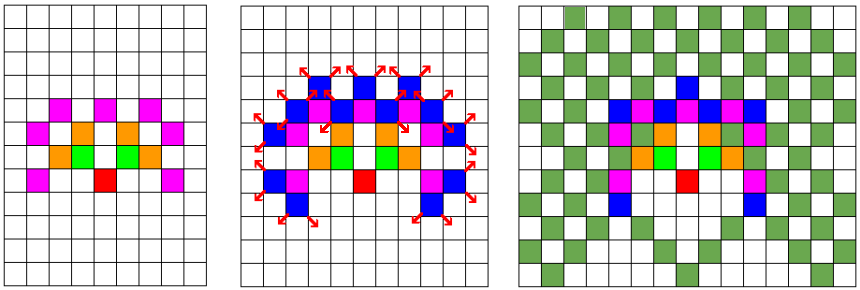
Для второго примера рисунки демонстрируют ситуацию на 4, 5 и 6 уровнях рекурсии. На рисунке посередине показаны направления всех частей, которые будут двигаться на следующем уровне.
| Название |
|---|




