| Codeforces Round 385 (Div. 1) |
|---|
| Закончено |
Учитель Коровоконга узнал, что тот весьма неплохо управляется с циклическими сдвигами, и придумал для него новую сложную задачу.
Вам дана последовательность из n строк s1, s2, ..., sn, которую мы обозначим как A.
Последовательность строк X называется стабильной, если выполнено условие, описанное ниже.
Для начала, сообщением назовём конкатенацию произвольного конечного количества элементов последовательности X. Любой элемент последовательности может быть использован произвольное количество раз, и конкатенация также происходит в произвольном порядке. Обозначим через SX множество всех возможных сообщений, которые можно построить по данной последовательности. Разумеется, это множество содержит бесконечно много элементов, если исходная последовательность X непуста.
Сообщение называется хорошим, если выполняются следующие условия:
- Допустим сообщение является конкатенацией k строк w1, w2, ..., wk, где каждое wi является элементом X.
- Рассмотрим все |w1| + |w2| + ... + |wk| возможных циклических сдвигов этой строки. Обозначим через m количество этих циклических сдвигов, являющихся элементами SX.
- Сообщение является хорошим, если и только если m в точности равно k.
Последовательность X называется стабильной, если и только если все элементы SX являются хорошими.
Пусть f(L) равно 1, если L является стабильной последовательностью, и 0 в противном случае.
Вычислите сумму f(L) по всем L, являющимся непустыми непрерывными подпоследовательностями A (всего существует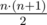 
непрерывных подпоследовательностей).
В первой строке входных данных записано целое число n (1 ≤ n ≤ 30), означающее количество строк в исходной последовательности.
Следующие n строк содержат строки si (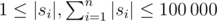
).
Выведите одно целое число, равное количеству непустых непрерывных подпоследовательностей, являющихся стабильными.
4
a
ab
b
bba
7
5
hh
ee
ll
ll
oo
0
6
aab
ab
bba
b
ab
c
13
В первом примере требуется рассмотреть 10 непрерывных подпоследовательностей. Не являются стабильными [«a», «ab», «b»], [«ab», «b», «bba»] и [«a», «ab», «b», «bba»]. Остальные семь являются стабильными.
Например, X = [«a», «ab», «b»] не является стабильной, поскольку у сообщения «ab» + «ab» = «abab» четыре циклических сдвига [«abab», «baba», «abab», «baba»], все из которых являются элементами SX.
