В прямоугольной комнате размером n на m метров расположено k датчиков, датчик номер i расположен в точке с координатами (xi, yi). Все датчики расположены в различных точках, находящихся строго внутри прямоугольника.
Противоположные углы комнаты находятся в точках с координатами (0, 0) и (n, m). Стены комнаты расположены параллельно осям координат.
В момент времени 0, из точки (0, 0) в направлении точки (1, 1) выпускается лазерный луч. Луч летит со скоростью 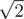 метров в секунду. Таким образом, луч окажется в точке (1, 1) ровно через одну секунду после старта.
метров в секунду. Таким образом, луч окажется в точке (1, 1) ровно через одну секунду после старта.
При столкновении со стеной луч отражается по закону, что угол падения равен углу отражения. При попадании луча в любой из четырёх углов комнаты он останавливается.
Определите для каждого датчика первый момент времени, когда луч пройдет сквозь точку, содержащую этот датчик. Для датчиков, через которые луч не пройдёт, выведите - 1.
В первой строке входных данных записаны три числа n, m и k (2 ≤ n, m ≤ 100 000, 1 ≤ k ≤ 100 000) — размеры комнаты и количество датчиков.
В следующих k строках записаны по два целых числа xi и yi (1 ≤ xi ≤ n - 1, 1 ≤ yi ≤ m - 1) — координаты датчиков. Гарантируется, что никакие два датчика не находятся в одной точке.
Выведите k целых чисел, i-е из которых должно равняться времени в секундах, через которое луч пройдёт через i-й датчик, или - 1, если этого не произойдёт.
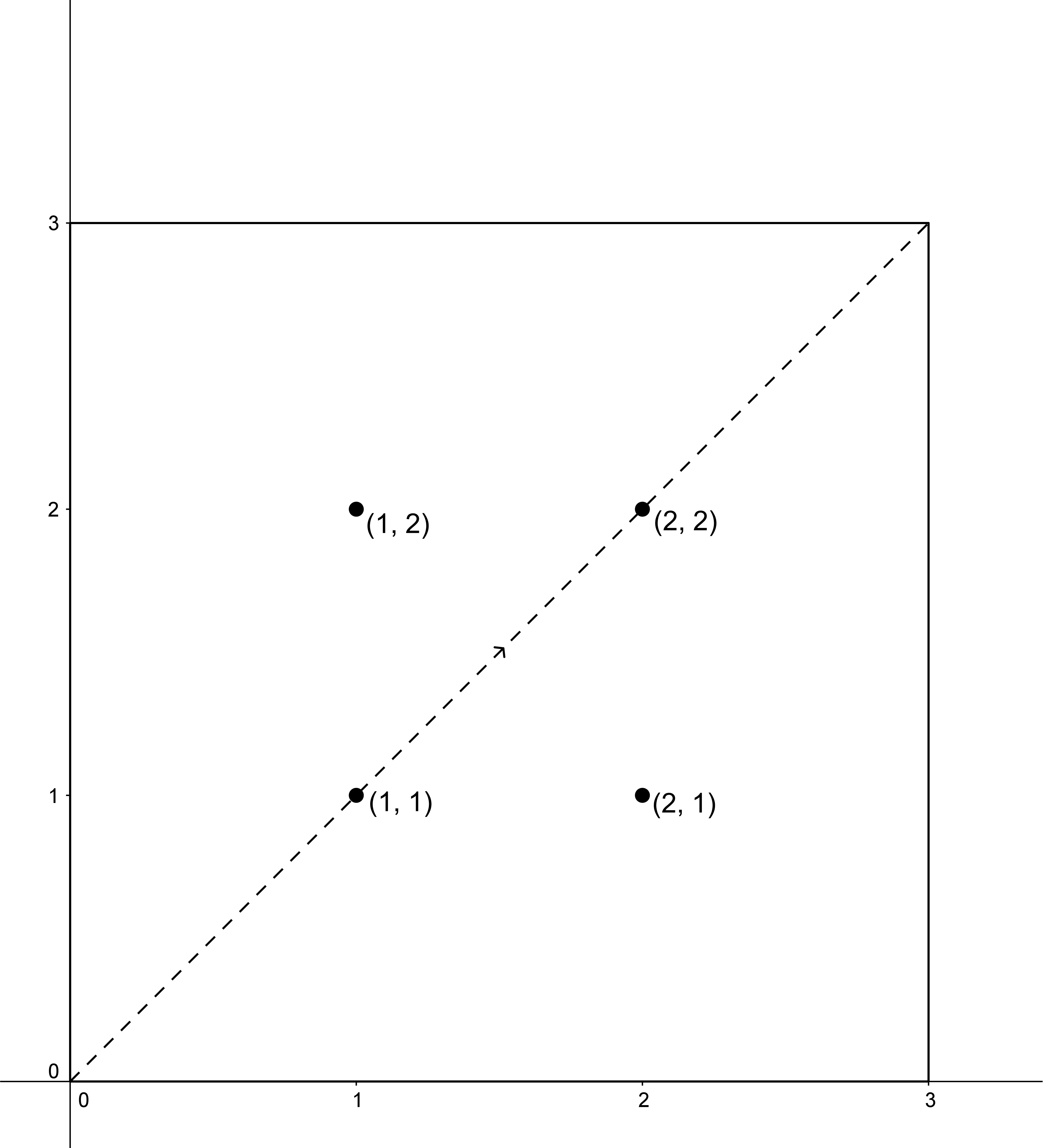
3 3 4
1 1
1 2
2 1
2 2
1
-1
-1
2
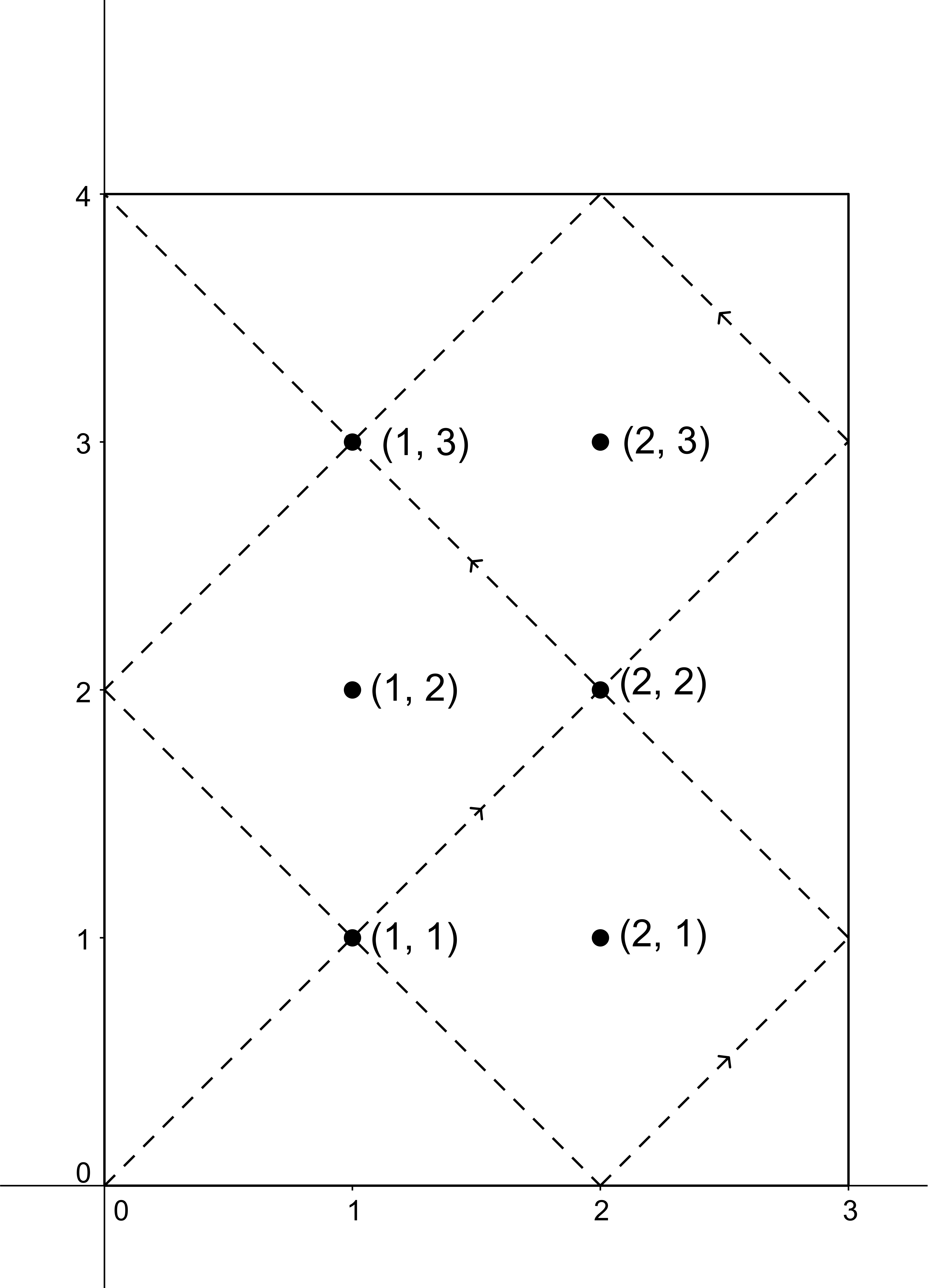
3 4 6
1 1
2 1
1 2
2 2
1 3
2 3
1
-1
-1
2
5
-1
7 4 5
1 3
2 2
5 1
5 3
4 3
13
2
9
5
-1
В первом примере луч пройдёт последовательно через точки со следующими координатами: (0, 0), (1, 1), (2, 2), (3, 3). Таким образом, через 3 секунды после вылета луч остановится в точке (3, 3).
Во втором примере луч пройдёт последовательно через точки со следующими коорданатами: (0, 0), (1, 1), (2, 2), (3, 3), (2, 4), (1, 3), (0, 2), (1, 1), (2, 0), (3, 1), (2, 2), (1, 3), (0, 4). В этом примере луч остановится в точке (0, 4) через 12 секунд после вылета. За это время он отразится от стен в точках (3, 3), (2, 4), (0, 2), (2, 0) и (3, 1).
| Название |
|---|




