| Codeforces Round 370 (Div. 2) |
|---|
| Закончено |
В ряд расположены n казино. Если Мемори играет в казино i, то с вероятностью pi она выигрывает и переходит в казино справа (i + 1) или уходит совсем (если i = n), а с вероятностью 1 - pi она проигрывает и двигается налево (i - 1) или тоже уходит (если i = 1).
Будем говорить, что Мемори доминирует на отрезке i... j, если её перемещения удовлетворяют следующим условиям:
- Она начинает в казино i.
- Она никогда не проигрывает в казино i.
- Она завершает путешествие по отрезку победой в казино j.
Обратите внимание, что если Мемори пойдет налево из казино 1 или направо из казино n, то её прогулка по казино сразу завершается.
Теперь Мемори хочет, чтобы вы обработали для неё несколько запросов:
- 1 i a b: присвоить
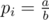 .
. - 2 l r: вывести вероятность того, что Мемори будет доминировать на отрезке l... r, то есть вероятность того, что, начав в казино l, она впервые выйдет за пределы отрезка l... r после победы в казино r.
Гарантируется, что в любой момент времени последовательность p неубывающая, то есть pi ≤ pi + 1 для всех i от 1 до n - 1.
В первой строке входных данных записаны два целых числа n и q (1 ≤ n, q ≤ 100 000) — количество казино и количество запросов соответственно.
В следующих n строках содержатся целые числа ai и bi (1 ≤ ai < bi ≤ 109) — дробь 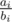 определяет вероятность pi выиграть в казино i.
определяет вероятность pi выиграть в казино i.
Следующие q строк содержат запросы в одном из двух видов, описанных в условии (1 ≤ a < b ≤ 109, 1 ≤ i ≤ n, 1 ≤ l ≤ r ≤ n).
Гарантируется, что во входных данных встретится хотя бы один запрос типа 2, то есть выходные данные будут не пусты. Дополнительно гарантируется, что в любой момент времени последовательность p является неубывающей.
Для каждого запроса типа 2 выведите одно вещественное число — вероятность того, что Мемори будет доминировать на соответствующем интервале. Ваш ответ будет считаться правильным, если его абсолютная ошибка не будет превосходить 10 - 4.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если |a - b| ≤ 10 - 4.
3 13
1 3
1 2
2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3
1 2 2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3
0.3333333333
0.2000000000
0.1666666667
0.5000000000
0.4000000000
0.6666666667
0.3333333333
0.2500000000
0.2222222222
0.6666666667
0.5714285714
0.6666666667
| Название |
|---|




