| AIM Tech Round 3 (Div. 1) |
|---|
| Закончено |
На экзамене в магистратуру Кибер-Механического факультета МГУ Саше попался билет про алгоритм Форда-Фалкерсона. Этот билет он знал очень хорошо, потому что неоднократно встречал алгоритм на олимпиадах. В качестве задачи к билету была дана сеть с уже частично построенным потоком, на которой надо было продемонстрировать работу алгоритма. Саша быстро написал билет и приступил было к задаче, как вдруг понял, что описание сети некорректное!
Ему был дан ориентированный граф G(V, E), в котором выделены две вершины s и t, называемые сток и исток. Обозначим за n количество вершин в графе, то есть n = |V|, а за m — количество рёбер в графе, то есть m = |E|. В рамках данной задачи будем полагать истоком вершину с номером 1, а стоком — вершину с номером n. Дополнительно, на рёбрах графа определена функция пропускных способностей c(e) и функция потока f(e). Функция f(e) определяет корректный поток, если выполнены следующие условия:
- Для любого ребра
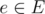поток по данному ребру неотрицателен и не превосходит c(e), то есть 0 ≤ f(e) ≤ c(e). - Для любой вершины
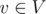, не являющейся стоком или истоком (v ≠ s и v ≠ t), суммарный поток по всем рёбрам, входящим в v, равен суммарному потоку по всем рёбрам, выходящим из v. Другими словами, поток не скапливается в вершине v.
Было понятно, что экзамен готовили в последнюю ночь, и поэтому в условие закралось много опечаток. Саша подошёл к преподавателю и попросил исправить сеть и дать корректную задачу, на что получил ответ — студенты магистратуры должны уметь исправить сеть сами. Чтобы Саша не упростил себе задачу, преподаватель сказал, что сумма всех изменений должна быть минимальной. Направление рёбер менять нельзя, их нельзя удалять или добавлять. Разрешается изменять только пропускные способности c(e) и величины потока f(e), причём все величины должны остаться целочисленными и неотрицательными. Полученное описание сети не обязательно должно быть максимальным потоком, его Саша позже найдет сам.
Найдите минимальную сумму всех изменений функций f(e) и c(e), которые придётся сделать Саше, чтобы функция потока стала корректной. Суммарное изменение считается как сумма абсолютной разницы, то есть если новые функции равны f * (e) и c * (e), то считается, что было внесено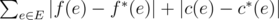 
изменений.
В первой строке входных данных записаны числа n и m (2 ≤ n ≤ 100, 0 ≤ m ≤ 100) — количество вершин и рёбер графа соответственно. В последующих m строках даны описания ребер, состоящие из четырёх целых чисел ui, vi, ci и fi (1 ≤ ui, vi ≤ n, ui ≠ vi, 0 ≤ ci, fi ≤ 1 000 000) — индекс вершины, из которой выходит ребро, индекс вершины, в которую входит ребро, пропускная способность ребра и текущий поток.
Истоком является вершина номер 1, а стоком — вершина номер n. Гарантируется, что в исток не входит ни одно ребро и ни одно ребро не выходит из стока.
Заданный граф не содержит петель, но может содержать кратные рёбра.
Выведите одно целое число — минимальную сумму изменений, которые надо сделать Саше, чтобы получить корректное описание сети.
2 1
1 2 2 1
0
2 1
1 2 1 2
1
3 3
1 2 1 1
2 3 2 2
1 3 3 3
1
4 2
2 3 1 1
3 2 1 1
0
В первом тестовом примере поток изначально правильный. Обратите внимание, что поток не максимальный, но максимальность и не требуется.
Во втором тестовом примере поток по единственному ребру превосходит пропускную способность. Существует два оптимальных решения: увеличить пропускную способность до 2 или уменьшить величину потока до 1.
В третьем тестовом примере в вершину 2 входит одна единица потока, а выходит две. Одно из возможных решений — уменьшить величину потока по второму ребру на 1.
В четвертом примере в графе есть изолированная циркуляция, и, согласно определению, этот поток корректен.
