| Codeforces Round 363 (Div. 1) |
|---|
| Закончено |
Дерево — это неориентированный связный граф без циклов.
Рассмотрим корневое неориентированное дерево, состоящее из n вершин, пронумерованных от 1 до n. Существует несколько способов представлять такие деревья. Одним из наиболее популярных является массив предков, состоящий из n чисел p1, p2, ..., pn, где pi означает предка вершины i (в рамках данной задачи корень дерева считается предком самого себя).
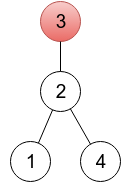 Для данного корневого дерева массив p равен [2, 3, 3, 2].
Для данного корневого дерева массив p равен [2, 3, 3, 2]. По данной последовательности p1, p2, ..., pn легко восстановить дерево:
- Существует ровно один индекс r, такой что pr = r. Вершина r является корнем дерева.
- Для всех остальных n - 1 вершины i существует ребро между вершинами i и pi.
Последовательность p1, p2, ..., pn является корректной, если описанная выше процедура определяет некоторое (произвольное) корневое дерево. Например, для n = 3 последовательности (1,2,2), (2,3,1) и (2,1,3) не являются корректными.
Вам дана последовательность a1, a2, ..., an, не обязательно являющаяся корректной. Вам требуется изменить минимальное количество элементов, чтобы последовательность стала корректной. Выведите минимальное необходимое количество изменений и пример любого ответа, который можно получить с их помощью. Если существует несколько корректных последовательностей, достижимых за минимальное количество изменений, то разрешается вывести любую.
В первой строке входных данных записано число n (2 ≤ n ≤ 200 000) — количество вершин в дереве (а значит, и в последовательности).
Во второй строке записаны n целых чисел a1, a2, ..., an (1 ≤ ai ≤ n).
В первой строке выведите минимальное количество изменений, которое надо сделать, чтобы получить корректную последовательность.
Во второй строке выведите любую корректную последовательность, которая может быть получена из (a1, a2, ..., an) за минимальное количество изменений. Если существует несколько таких последовательностей, то выведите любую.
4
2 3 3 4
1
2 3 4 4
5
3 2 2 5 3
0
3 2 2 5 3
8
2 3 5 4 1 6 6 7
2
2 3 7 8 1 6 6 7
В первом примере достаточно изменить один элемент. В приведённом примере вывода последовательность представляет корневое дерево с корнем в вершине 4 (потому что p4 = 4), которое можно увидеть на левом рисунке. Одним из корректных решений будет являться последовательность 2 3 3 2, определяющая дерево с корнем в вершине 3 (правый рисунок). На обоих рисунках корни выделены красным.

Во втором примере данная во входных данных последовательность уже является корректной.
| Название |
|---|




