| Educational Codeforces Round 14 |
|---|
| Закончено |
Вам задано n целых чисел a1, a2, ..., an.
Последовательность целых чисел x1, x2, ..., xk называется "xor-последовательностью", если для всех 1 ≤ i ≤ k - 1 количество единиц в двоичном представлении числа xi  xi + 1 кратно трём и
xi + 1 кратно трём и 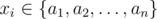 для всех 1 ≤ i ≤ k. Знак
для всех 1 ≤ i ≤ k. Знак  обозначает операцию двоичного исключающего или.
обозначает операцию двоичного исключающего или.
Найдите количество "xor-последовательностей" длины k по модулю 109 + 7.
Обратите внимание, если a = [1, 1] и k = 1, то ответ равен 2, поскольку вы должны рассматривать единицы из a как разные.
В первой строке находится пара целых чисел n и k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — количество заданных целых чисел и длина "xor-последовательностей".
Во второй строке находятся n целых чисел ai (0 ≤ ai ≤ 1018).
Выведите единственное число c — количество "xor-последовательностей" длины k по модулю 109 + 7.
5 2
15 1 2 4 8
13
5 1
15 1 2 4 8
5
| Название |
|---|




