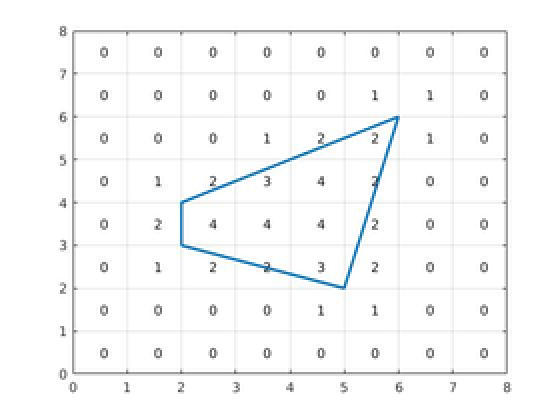
Теперь, когда Хайди убедилась, что её тестер уровня загрязнения зомби работает, пора наносить удар! В этот раз, убежище зомби представляет собой строго выпуклый многоугольник на решётке. Каждая вершина многоугольника находится в каком-то узле решётки. Для каждой клетки решётки Хайди знает уровень загрязнения зомби — количество углов клетки, которые находятся внутри или на границе решётки.
По данной информации Хайди хочет определить точную форму убежища, чтобы обрушить на зомби справедливое возмездие, помогите ей в этом!
Входные данные содержат несколько тестов.
В первой строке каждого теста записано целое число n — размер решётчатого поля (5 ≤ n ≤ 500). В каждой из последующих n строк записаны n символов, описывающих уровень загрязнения зомби в каждой из клеток поля. Каждый символ каждой строки является цифрой от 0 до 4.
Клетки даны в том же порядке, что и на картинке выше: строки нумеруются в порядке уменьшения y координаты, и в каждом ряду клетки даны в порядке увеличения x координаты. Это означает, что первый ряд соответствует клеткам с координатами (1, n), ..., (n, n), а последний ряд соответствует клеткам с координатами (1, 1), ..., (n, 1).
В последней строке файла записан ноль. Эта строка служит сигналом конца ввода и не должна обрабатываться как отдельный тест. Сумма значений n по всем тестам в файле не превзойдёт 5000.
Для каждого теста выведите ответ в следующем виде:
в первой строке выведите целое число v — количество вершин в многоугольнике, являющемся секретным убежищем. В следующих v строках выведите по два целых числа, определяющих вершины многоугольника в порядке обхода по часовой стрелке, начиная с лексикографически минимальной вершины.
8
00000000
00000110
00012210
01234200
02444200
01223200
00001100
00000000
5
00000
01210
02420
01210
00000
7
0000000
0122100
0134200
0013200
0002200
0001100
0000000
0
4
2 3
2 4
6 6
5 2
4
2 2
2 3
3 3
3 2
3
2 5
4 5
4 2
Гарантируется, что решение всегда существует и единственно. Гарантируется, что в корректном решении вершины многоугольника имеют координаты между 2 и n - 2. Вершины (x1, y1) лексикографически меньше вершины (x2, y2) если x1 < x2 или 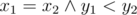 .
.
| Название |
|---|




