| Codeforces Round 360 (Div. 1) |
|---|
| Закончено |
Давным-давно существовало великое королевство, которым правили Великий Арий и Пари Великая. У этих двоих были некоторые разногласия по вопросу любимых чисел, поэтому они решили разделить королевство между собой.
Великое королевство состояло из n городов, пронумерованных целыми числами от 1 до n, и m двунаправленных дорог, пронумерованных от 1 до m. Длина i-й из этих дорог равняется wi. Великий Арий и Пари Великая договорились уничтожить некоторый префикс дорог (все дороги с номером меньше некоторого x) и некоторый суффикс дорог (все дороги с номером больше некоторого x), оставив таким образом дороги с номерами l, l + 1, ..., r - 1 и r.
После этого они разделят королевство на две части (каждый город отойдёт ровно к одной из двух частей), такие что трудность разделения будет минимальна. Трудностью разделения называется максимальная длина дороги, такой что оба её конца принадлежат одной части. В случае если таких дорог вообще нет, трудность разделения полагается равной - 1.
Историки обнаружили карту великого королевства и теперь обсуждают q возможных сценариев выбора параметров l и r великими правителями. По имеющимся данным для каждой гипотезы li, ri определите минимально возможную трудность разделения королевства.
В первой строке входных данных записаны три целых числа n, m и q (1 ≤ n, q ≤ 1000,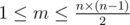 
) — количество городов и дорог в великом королевстве и количество гипотез историков соответственно.
В i-й из последующих m строк записаны три целых числа ui, vi и wi (1 ≤ ui, vi ≤ n, 0 ≤ wi ≤ 109), обозначающих, что дорога с номером i соединяет города ui и vi и имеет длину wi. Гарантируется, что никакая дорога не соединяет город с самим собой и никакие две дороги не соединяют одну и ту же пару городов.
В каждой из последующих q строк записаны два целых числа li и ri (1 ≤ li ≤ ri ≤ m) — догадка историков об оставшихся в королевстве дорогах.
Для каждой догадки историков выведите минимально возможную трудность разделения королевства.
5 6 5
5 4 86
5 1 0
1 3 38
2 1 33
2 4 28
2 3 40
3 5
2 6
1 3
2 3
1 6
-1
33
-1
-1
33
