| Codeforces Round 356 (Div. 1) |
|---|
| Закончено |
В Беарляндии n городов, пронумерованных целыми числами от 1 до n. Они соединены m двунаправленными дорогами. Дорога номер i соединяет два различных города ai и bi, и никакие две дороги не соединяют одну и ту же пару городов. От любого города можно добраться до любого другого, используя только данные дороги.
Расстоянием между городами a и b называется минимальное количество дорог, которыми придётся воспользоваться, чтобы попасть из a в b.
Лимак — медведь гризли. Он преступник, и ваша задача его поймать, или, по крайней мере, попытаться. У вас осталось только два дня (сегодня и завтра), а затем он улизнёт навсегда.
Ваше главное оружие — БВД (Беарляндский Высокоточный Детектор). Когда вы используете БВД, находясь при этом в каком-нибудь городе, он сообщает вам расстояние между городом, где вы находитесь, и городом, где сейчас находится Лимак. К сожалению, БВД может быть использован только один раз в день.
Вам мало что известно о местоположении Лимака, поэтому вы предполагаете, что он находится в одном из n городов страны, выбранном случайно и с равной вероятностью (то есть Лимак изначально находится в каждом городе с вероятностью  ). Вы разработали следующий план:
). Вы разработали следующий план:
- Выбрать один из городов и применить там БВД.
- Сразу после применения БВД можно попытаться поймать Лимака (но это может быть плохой идеей). В этом случае вы выбираете какой-то город и ищете Лимака там. Если Лимак действительно в этом городе, то вы выигрываете, в противном случае Лимак становится осторожнее, и его уже никогда не поймать (вы проигрываете).
- Подождать 24 часа и снова применить БВД. Вы знаете, что за это время Лимак обязательно изменит своё местоположение, а именно, он выберет случайно и равновероятно одну дорогу ведущую из его текущего города и пройдёт по ней в соседний город.
- На следующий день вы можете снова выбрать любой город и применить БВД там.
- Теперь уже обязательно попробовать поймать Лимака. Для этого вы выбираете какой-то город и ищете в нём Лимака. Если он там, то вы побеждаете, если нет — проигрываете.
Каждый раз, когда вам требуется выбрать город, вы можете выбирать любой из n городов, то есть мгновенное перемещение не является для вас проблемой.
Чему равна вероятность поймать Лимака, если вы будете действовать оптимально?
В первой строке входных данных записаны два числа n и m (2 ≤ n ≤ 400, 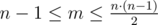 ) — количество городов и количество дорог соответственно.
) — количество городов и количество дорог соответственно.
Затем следуют m строк, описывающих дороги. В i-й из этих строк записаны два числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi) — номера городов, соединённых i-й дорогой.
Гарантируется, что никакая пара городов не соединена более чем одной дорогой и что от любого города можно добраться до любого другого, используя только данные дороги.
Выведите одно вещественное число — вероятность обнаружить Лимака, если действовать оптимально. Ваш ответ будет считаться правильным, если его абсолютная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если |a - b| ≤ 10 - 6.
3 3
1 2
1 3
2 3
0.833333333333
5 4
1 2
3 1
5 1
1 4
1.000000000000
4 4
1 2
1 3
2 3
1 4
0.916666666667
5 5
1 2
2 3
3 4
4 5
1 5
0.900000000000
В первом примере Беарляндия состоит из трёх городов, и между каждой парой этих городов есть дорога. Рассмотрим один из оптимальных сценариев.
- Использовать БВД в городе 1.
- С вероятностью
 Лимак окажется в этом городе, и БВД выдаст расстояние 0. В таком случае нужно сразу хватать Лимака — мы точно не ошибёмся.
Лимак окажется в этом городе, и БВД выдаст расстояние 0. В таком случае нужно сразу хватать Лимака — мы точно не ошибёмся. - С вероятностью
 расстояние равно 1, потому что Лимак находится в городе 2 или городе 3. В этом случае оптимально будет дождаться следующего дня.
расстояние равно 1, потому что Лимак находится в городе 2 или городе 3. В этом случае оптимально будет дождаться следующего дня.
- С вероятностью
- Вы ждёте, а Лимак переходит в соседний город.
- С вероятностью
 Лимак находился в городе 2 и перешёл в город 3.
Лимак находился в городе 2 и перешёл в город 3. -
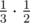 он перешёл из 2 в 1.
он перешёл из 2 в 1. -
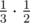 он перешёл из 3 в 2.
он перешёл из 3 в 2. -
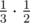 он перешёл из 3 в 1.
он перешёл из 3 в 1.
- С вероятностью
- Снова использовать БВД в городе 1 (хотя разрешено сделать это и в любом другом городе).
- Если расстояние 0, то Лимак находится в городе 1 (вы побеждаете).
- Если расстояние 1, то Лимак либо в городе 2, либо в городе 3. Тогда попробуем поискать его в городе 2 (или 3, не имеет значения).
Пользуясь такой стратегией, вы проиграете, только если Лимак был изначально в городе 2 и перешёл в город 3. Вероятность проигрыша равна 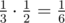 . Ответ равен
. Ответ равен  .
.
| Название |
|---|




