| Manthan 2011 |
|---|
| Закончено |
В городе Аалам-Аара (по-русски Свет Земли), ранее не было ни преступлений, ни преступников, но течением времени грехи поселились в сердцах некогда праведных людей. В поисках решения этой проблемы некоторые из старейшин обнаружили, что до тех пор, пока испорченную часть населения держат подальше от неиспорченной, преступления можно остановить. Итак, они решили переселить всех испорченных людей на отдельную территорию. Для того, чтобы преступники наверняка не смогли сбежать из отделенной части, небходимо соорудить сторожевую башню, чтобы можно было наблюдать за преступниками.
Коль скоро народ Аалам-Аара не очень богат, то они встретились с купцом из некоторого богатого города, который согласился продать им земельный участок, огражденный высоким забором по периметру. Забор представляет собой многоугольник (не обязательно выпуклый). На одной из частей забора, отрезке AB есть сооружения, где можно построить смотровую башню. Ваша задача — помочь им узнать количество точек вдоль этого забора, где можно построить башню, чтобы оттуда можно было наблюдать за всеми преступниками. Можно построить только одну сторожевую башню. За преступником можно наблюдать из сторожевой башни, если отрезок видимости от сторожевой башни до преступника нигде не пересекает забор, т.е. целиком расположен внутри или на границы области. Как показано на рисунке 1 ниже, точки Y, C и A видны из точки B, а точки E и D не видны.
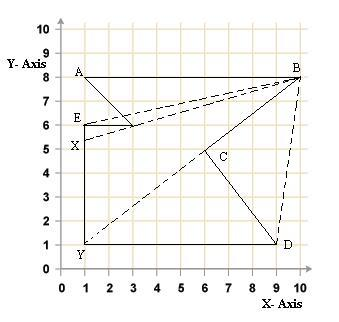 Рис. 1
Рис. 1  Рис. 2
Рис. 2 Предположим, что земельный участок является многоугольника и оси координат установлены так, что отрезок AB параллелен оси X, а точки, где можно построить сторожевую башню, — это целочисленные точки на отрезке AB. Например, на данном рисунке 2, сторожевую башню можно установить в любой из пяти целочисленных точек на AB, то есть в точках (4, 8), (5, 8), (6, 8), (7, 8), или (8, 8). Можно считать, что никакие три последовательные точки не лежат на одной прямой и все угловые точки, отличные от A и B, лежат по одну сторону забора AB. Многоугольник не содержит самопересечений.
Первая строка теста содержит количество вершин n (3 ≤ n ≤ 1000).
Следующие n строк содержат координаты вершин многоугольника в порядке следования по часовой стрелке. На i-ой строке записаны через пробел целые числа xi и yi (0 ≤ xi, yi ≤ 106).
Конечные точки забора AB — это первые две точки, (x1, y1) и (x2, y2).
Выходные данные состоят из единственной строки, в которой содержится число точек, в которых можно построить смотровую башню.
5
4 8
8 8
9 4
4 0
0 4
5
5
4 8
5 8
5 4
7 4
2 2
0
Рисунок 2 показывает первый тест. Все точки на рисунке обозреваемы с любой точки на заборе AB. Так как AB имеет 5 целочисленных координат, значит, ответ равен 5.
Во втором тесте заборы CD и DE не видны полностью, таким образом, ответ равен 0.
| Название |
|---|




