| Codeforces Round 349 (Div. 2) |
|---|
| Закончено |

Как некоторые знают, кубизм — направление в живописи, в котором на первый план выходит задача конструирования объёмной формы на плоскости с помощью комбинации трёхмерных геометрических фигур.
Знаменитый скульптор Кикассо, чей автопортрет вы можете лицезреть, ненавидит кубизм. Ему гораздо больше импонирует идея передачи двумерных объектов через трехмерные с помощью своих великолепных скульптур. И его новый проект связан именно с этим. Кикассо собирается сделать герб обществу ненавистников кубизма. Для этого он хочет создать скульптуру, изображающую всем известный геометрический примитив — выпуклый многоугольник.
Кикассо подготовил для этого несколько заготовок, представляющих собой стержни с целочисленными длинами, и теперь он хочет собрать их воедино, причём i-й стержень представляет собой отрезок прямой длины li.
Скульптор планирует составить выпуклый многоугольник ненулевой площади, используя все имеющиеся стержни в качестве его сторон. Каждый стержень необходимо использовать в качестве стороны на его полную длину. Резать, ломать или сгибать стержни нельзя. Однако, две стороны могут образовывать развернутый угол в 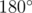 .
.
Увы, как и многие другие гениальные личности своего времени, он рано бросил учёбу. Поэтому Кикассо не знал, что сложить выпуклый многоугольник ненулевой площади из стержней тех длин, которые он выбрал никак не получится. Не желая оставлять стержни неиспользованными, скульптор решил, что сделает ещё одну заготовку-стержень с целочисленной длиной так, чтобы его проблема решилась. При этом он, конечно, хочет сделать её как можно более короткой, ведь материалы дорогие, и тратить деньги общества зря — неподобающее дело.
Помогите скульптору!
В первой строке находится целое число n (3 ≤ n ≤ 105) — количество заготовок-стержней.
Во второй строке находятся n целых чисел li (1 ≤ li ≤ 109) — длины стержней, которые уже есть у Кикассо. Гарантируется, что нельзя составить выпуклый n-угольник ненулевой площади с помощью имеющихся у Кикассо стержней, используя их в качестве сторон.
Выведите единственное целое число — минимальную длину стержня, при добавлении которого из всех стержней можно будет сложить выпуклый (n + 1)-угольник ненулевой площади.
3
1 2 1
1
5
20 4 3 2 1
11
В первом примере можно составить из набора длин {1, 1, 1, 2} треугольник со сторонами {1 + 1 = 2, 2, 1}.
Во втором примере можно составить треугольник с длинами {20, 11, 4 + 3 + 2 + 1 = 10}.
| Название |
|---|




