| Educational Codeforces Round 11 |
|---|
| Закончено |
Лимак — старый бурый медведь. Он часто играет в боулинг со своими друзьями. Сегодня он в отличном настроении и хочет побить свой собственный рекорд!
За каждый бросок даётся некоторое целое (возможно отрицательное) количество очков. Очки за i-й бросок умножаются на число i и прибавляются к общей сумме. Таким образом, за k бросков с очками s1, s2, ..., sk в сумме даётся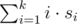 
очков. Если бросков не было, общее количество очков равно 0.
Лимак сделал n бросков и получил ai очков за i-й бросок. Он хочет максимизировать общее количество очков, поэтому ему в голову пришла интересная идея. Он может сказать, что некоторое количество первых бросков он разогревался и был рассредоточен во время некоторого количества последних бросков. Формально он может выкинуть некоторый префикс и некоторый суффикс последовательности очков a1, a2, ..., an. Разрешается выкидывать из рассмотрения все броски или же не выкидывать из вовсе.
Общее количество очков вычисляется как будто выкинутых бросков не было. Таким образом, за первый невыкинутый бросок количество очков умножается на 1, за второй — на 2 и так далее до последнего невыкинутого броска.
Какое максимальное количество очков может получить Лимак?
В первой строке находится целое число n (1 ≤ n ≤ 2·105) — общее количество бросков, сделанных Лимаком.
Во второй строке находятся n целых чисел a1, a2, ..., an (|ai| ≤ 107) — очки полученные Лимаком.
Выведите максимальное суммарное количество очков, которое можно получить выкидыванием некоторых бросков.
6
5 -1000 1 -3 7 -8
16
5
1000 1000 1001 1000 1000
15003
3
-60 -70 -80
0
В первом примере Лимак должен выкинуть из рассмотрения первые два и последний броски. После этого останутся броски 1, - 3, 7, которые принесут ему 1·1 + 2·( - 3) + 3·7 = 1 - 6 + 21 = 16 очков.
