| Чемпионат КРОК 2016 - Отборочный Раунд |
|---|
| Закончено |
Пока Фермер Джон строит новую ферму в незнакомой части Бовинии, Бесси решила попробовать себя в новом деле. Она стала репортёром и отвечает в местной газете за репортажи с различных IT-соревнований. Сейчас она освещает результаты Турнира Роботов-Рэперов 2016. Она быстро заметила, что в результатах матчей нет никакой случайности: робот i всегда победит робота j, если его умение читать рэп выше. Если робот i побеждает робота j, и робот j побеждает робота k, то робот i гарантированно победит робота k. Читать рэп такое тонкое искусство, что уровень этого умения у всех роботов разный.
Вам даны результаты матчей в порядке, в котором эти матчи проходили. Определите минимальное количество первых матчей, после которых Бесси уже однозначно может упорядочить роботов по уровню умения читать рэп.
В первой строке входных данных записаны два числа n и m (2 ≤ n ≤ 100 000,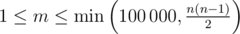 
) — количество роботов и количество матчей соответственно.
Следующие m строк описывают результаты матчей в порядке, в котором эти матчи проходили. Каждая строка содержит два индекса ui и vi (1 ≤ ui, vi ≤ n, ui ≠ vi), означающих, что робот номер ui победил робота номер vi в i-м матче. Никакая пара роботов не соревновалась дважды.
Гарантируется, что существует хотя бы один порядок роботов, удовлетворяющий всем m результатам.
Выведите минимальное k, такое что результатов первых k матчей достаточно, чтобы однозначно упорядочить роботов по умению читать рэп. Если существует больше одного порядка роботов, удовлетворяющего результатам всех m матчей, выведите -1.
4 5
2 1
1 3
2 3
4 2
4 3
4
3 2
1 2
3 2
-1
В первом примере роботы могут быть упорядочены от сильнейшего к слабейшему следующим образом: (4, 2, 1, 3). Бесси может однозначно определить этот порядок, зная результаты первых четырёх матчей.
Во втором примере оба порядка (1, 3, 2) и (3, 1, 2) подойдут под результаты всех матчей.
