| Codeforces Round 343 (Div. 2) |
|---|
| Закончено |
Карта города, в котором живёт Фома Дор, представляет собой дерево (неориентированный связный граф без простых циклов), поэтому гости зовут его Древоградом. В городе n перекрёстков, соединённых n - 1 дорогой. По всем дорогам можно перемещаться в обоих направлениях.
В городе живёт m друзей Фомы Дора, i-й из них живёт рядом с перекрёстком ui, а работает рядом с перекрёстком vi. Все жители города несчастны, потому что между из домом и работой существует ровно один простой путь.
Фома Дор хочет построить ровно одну новую дорогу, которую он выберет случайно среди всех n·(n - 1) / 2 возможных дорог. Обратите внимание, что он вполне может построить новую дорогу между какой-то парой перекрёстков, уже соединённых друг с другом дорогой.
Фома знает, что каждый из его друзей будет счастлив, если после построения новой дороги будет путь из его дома до работы и обратно, который не проходит по одной дороге дважды. Формально, в графе будет существовать простой цикл, на котором лежат ui и vi.
Более того, если какой-то друг становится счастлив, то уровень его радости определяется как длина этого пути (несложно заметить, что эта длина определяется однозначно). Для каждого своего друга Фома хочет вычислить математическое ожидание значения уровня радости, то есть математическое ожидание длины цикла, если этот цикл содержит ui и vi.
В первой строке входных данных записаны числа n и m (2 ≤ n, m ≤ 100 000) — количество перекрёстков в Древограде и друзей Фомы соответственно.
Далее следует n - 1 строка с описанием дорог. Каждая строка содержит два числа ai и bi (1 ≤ ai, bi ≤ n) — индексы перекрёстков, соединённых i-й дорогой.
В последних m строках описываются друзья Фомы Дора. В i-й из этих строк записаны два числа ui и vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — номер перекрёстка, где живёт i друг, и номер перекрёстка, где он работает.
Для каждого друга Фомы Дора вычислите математическое ожидание его уровня радости, при условии, что он будет счастлив. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 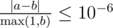 .
.
4 3
2 4
4 1
3 2
3 1
2 3
4 1
4.00000000
3.00000000
3.00000000
3 3
1 2
1 3
1 2
1 3
2 3
2.50000000
2.50000000
3.00000000
Рассмотрим второй пример.
- Подходят дороги (1, 2) и (2, 3), поэтому математическое ожидание равняется
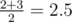
- Построение дорог (1, 3) и (2, 3) сделает второго друга счастливым. Как и для друга 1, ответ равен 2.5
- Единственный способ сделать третьего друга счастливым — это построить дорогу (2, 3), поэтому ответ равен 3
| Название |
|---|




