| 8VC Venture Cup 2016 - Elimination Round |
|---|
| Закончено |
Эндрю и Джерри играют в игру, а Гарри ведёт счёт. Игра состоит из трёх раундов. В каждом раунде Эндрю и Джерри по очереди вынимают по одному шару из урны, содержащей n шаров, на которых написаны различные целые числа. Затем они передают шары Гарри, который добавляет очко тому, на чьём шаре было написано большее число, и кладёт их обратно в урну. Победителем игры объявляется тот, кто выиграл хотя бы в двух раундах из трёх.
Известно, что Эндрю выиграл в раундах 1 и 2, а Джерри победил в раунде 3, так что победителем игры стал Эндрю. Однако Джерри недоволен способом определения победителя — по его словам, сумма чисел на вытянутых им шарах была строго больше суммы чисел на шарах, вытянутых Эндрю. Какова вероятность такого события?
В первой строке входных данных записано единственное число n (2 ≤ n ≤ 2000) — количество шаров в урне.
Во второй строке записаны n целых чисел ai (1 ≤ ai ≤ 5000) — числа, написанные на шарах. Гарантируется, что все ai различны.
Выведите единственное вещественное число — вероятность того, что сумма чисел на всех шарах, вытянутых Джерри, была строго больше суммы чисел на всех шарах, вытянутых Эндрю, если известно, что Эндрю выиграл первые два раунда, а Джерри выиграл третий раунд. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 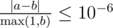 .
.
2
1 2
0.0000000000
3
1 2 10
0.0740740741
В первом примере имеется всего два шара. В первых двух раундах Эндрю обязательно доставал шар с числом 2, а Джерри доставал шар с числом 1, и наоборот в последнем раунде. Таким образом, сумма на всех шарах Эндрю обязательно равна 5, а на всех шарах Джерри — 4.
Во втором примере у каждой игры могло быть три исхода: 10 - 2, 10 - 1 или 2 - 1. Чтобы выполнилось условие на сумму, Эндрю обязательно должен был оба раза победить с исходом 2 - 1, а в последнем раунде Джерри должен был достать 10. Вероятность такого события равняется 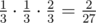 .
.
| Название |
|---|




