| Codeforces Round 341 (Div. 2) |
|---|
| Закончено |
В подчинении у Мокрой Акулы находится n акул, сидящих за круглым столом. Таким образом, соседями являются акулы с номерами i и i + 1 для всех i от 1 до n - 1, а так же акулы с номерами 1 и n.
Каждая акула в течение дня вырастит случайное количество цветков si — целое число от li до ri, при этом все варианты равновероятны. У Мокрой Акулы есть любимое простое число p, от которого он совершенно без ума! Если для какой-то пары соседних акул i и j произведение количества выращенных ими цветков si·sj делится на p, то Мокрая Акула радуется и даёт каждой из этих акул по 1000 бурлей.
В конце дня акулы собираются вместе и складывают все подаренные бурли. Вычислите математическое ожидание этого количества.
В первой строке входных данных записаны целые числа n и p (3 ≤ n ≤ 100 000, 2 ≤ p ≤ 109) — количество акул и любимое простое число Мокрой Акулы соответственно. Гарантируется, что p является простым числом.
Каждая из последующих n строк содержит описание одной акулы. В i из них записаны числа li и ri (1 ≤ li ≤ ri ≤ 109) — диапазон возможного количества цветов, выращенных i-й акулой. Не забудьте, что реальное количество цветов выбирается равновероятно на этом отрезке, включая границы.
Выведите единственное вещественное число — математическое ожидание суммарного количества бурлей, которое получат акулы. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 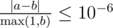 .
.
3 2
1 2
420 421
420420 420421
4500.0
3 5
1 4
2 3
11 14
0.0
Положительное целое число называется простым, если оно не делится ни на какое другое положительное целое число, кроме себя и 1. При этом число 1 простым не является.
Рассмотрим первый пример из условия. Первая акула выращивает от 1 до 2 цветков, вторая от 420 до 421, а третья от 420420 до 420421. Возможны восемь вариантов количества выращенных цветков (s0, s1, s2):
- (1, 420, 420420): 1·420 = 420, 420·420420 = 176576400 и 420420·1 = 420420. Каждая акула в каждой паре получит по 1000 бурлей, то есть в итоге каждая акула получит по 2000 бурлей, и сумма будет равна 6000 бурлей.
- (1, 420, 420421): В этом варианте 420421·1 не делится на 2, поэтому первая и третья акулы получат только по 1000 бурлей, а вторая всё ещё получит 2000. Итоговая сумма — 4000 бурлей.
- (1, 421, 420420): сумма 4000
- (1, 421, 420421): сумма 0.
- (2, 420, 420420): сумма 6000.
- (2, 420, 420421): сумма 6000.
- (2, 421, 420420): сумма 6000.
- (2, 421, 420421): сумма 4000.
Математическое ожидание равняется 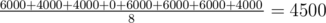 .
.
Во втором примере никакая комбинация количества цветов не приносит акулам бурлей.
| Название |
|---|




