| Codeforces Round 336 (Div. 1) |
|---|
| Закончено |
У Геноса есть n различных прямых на Декартовой плоскости. Обозначим как 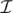 список всех точек пересечения данных прямых. Каждая точка появляется в списке столько раз, сколько пар прямых в ней пересекаются. Порядок точек в списке значения не имеет.
список всех точек пересечения данных прямых. Каждая точка появляется в списке столько раз, сколько пар прямых в ней пересекаются. Порядок точек в списке значения не имеет.
Для некоторой точки (p, q) обозначим как 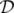 список расстояний от соответствующих точек в
список расстояний от соответствующих точек в 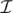 до точки (p, q). Под расстоянием здесь имеется в виду Евклидово расстояние. На всякий случай напомним, что Евклидово расстояние между двумя точками (x1, y1) и (x2, y2) равно
до точки (p, q). Под расстоянием здесь имеется в виду Евклидово расстояние. На всякий случай напомним, что Евклидово расстояние между двумя точками (x1, y1) и (x2, y2) равно 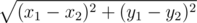 .
.
Теперь Геносу дана точка (p, q) и положительное целое число m. Его просят найти сумму m минимальных элементов в 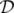 . Не следует рассматривать только уникальные элементы, то есть каждое число может войти в ответ столько раз, сколько оно встречается в
. Не следует рассматривать только уникальные элементы, то есть каждое число может войти в ответ столько раз, сколько оно встречается в 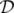 . Генос боится задач Div1 E, поэтому попросил вас помочь ему.
. Генос боится задач Div1 E, поэтому попросил вас помочь ему.
В первой строке входных данных записано единственное число n (2 ≤ n ≤ 50 000) — количество прямых.
Вторая строка содержит три целых числа x, y и m (|x|, |y| ≤ 1 000 000, 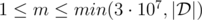 ) — закодированные координаты точки запроса, и целое число m, описанное в условии выше. Точка запроса (p, q) равна
) — закодированные координаты точки запроса, и целое число m, описанное в условии выше. Точка запроса (p, q) равна 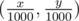 . Иными словами, разделите x и y на 1000, чтобы получить вещественную точку запроса.
. Иными словами, разделите x и y на 1000, чтобы получить вещественную точку запроса. 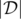 означает длину списка
означает длину списка 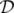 , при этом гарантируется, что
, при этом гарантируется, что 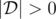 .
.
В каждой из следующих n строк записано по два целых числа ai и bi (|ai|, |bi| ≤ 1 000 000) — параметры прямой 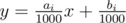 . Гарантируется, что никакие две прямые не совпадают, то есть (ai, bi) ≠ (aj, bj) if i ≠ j.
. Гарантируется, что никакие две прямые не совпадают, то есть (ai, bi) ≠ (aj, bj) if i ≠ j.
Выведите единственное вещественное число — сумму m минимальных элементов  . Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 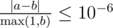 .
.
4
1000 1000 3
1000 0
-1000 0
0 5000
0 -5000
14.282170363
2
-1000000 -1000000 1
1000000 -1000000
999999 1000000
2000001000.999999500
3
-1000 1000 3
1000 0
-1000 2000
2000 -1000
6.000000000
5
-303667 189976 10
-638 116487
-581 44337
1231 -756844
1427 -44097
8271 -838417
12953.274911829
В первом примере три самые близкие к (1, 1) точки пересечения прямых имеют расстояния 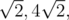 и
и 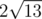 .
.
Во втором примере две прямые y = 1000x - 1000 и 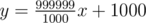 пересекаются в точке (2000000, 1999999000). Расстояние от этой точки до ( - 1000, - 1000) равно
пересекаются в точке (2000000, 1999999000). Расстояние от этой точки до ( - 1000, - 1000) равно 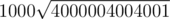 .
.
| Название |
|---|




