| Codeforces Round 333 (Div. 1) |
|---|
| Закончено |
Дано дерево T состоящее из n вершин (пронумерованных целыми числами от 1 до n). В каждой вершине записана некоторая буква. Корень дерева расположен в вершине 1.
Рассмотрим поддерево дерево Tv некоторой вершины v. Вдоль любого просто пути, начинающегося в v и заканчивающегося в некоторой вершине 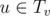 (возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как
(возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как 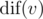 .
.
Дополнительно: для каждой вершины v дано целое число cv. Нас интересуют вершины, в которых значение 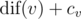 как можно больше.
как можно больше.
Вы должны вычислить две величины — максимальное значение 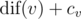 и количество вершин v с максимальным
и количество вершин v с максимальным 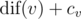 .
.
В первой строке входных данных записано единственное целое число n (1 ≤ n ≤ 300 000) — количество вершин в дереве T.
Во второй строке записано n целых чисел ci (0 ≤ ci ≤ 109).
В третьей строке записана строка s, состоящая из n строчных букв английского алфавита, — i-й символ этой строки соответствует букве, записанной в вершине i.
Далее следует n - 1 строка с описанием рёбер дерева T. Каждая из них содержит два целых числа u и v (1 ≤ u, v ≤ n), обозначающих ребро, которое соединяет вершины u и v.
Гарантируется, что входные данные описывают дерево.
Выведите два числа — значение 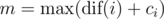 для всех 1 ≤ i ≤ n и количество вершин v, для которых
для всех 1 ≤ i ≤ n и количество вершин v, для которых 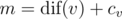 .
.
10
1 2 7 20 20 30 40 50 50 50
cacabbcddd
1 2
6 8
7 2
6 2
5 4
5 9
3 10
2 5
2 3
51
3
6
0 2 4 1 1 1
raaaba
1 2
2 3
2 4
2 5
3 6
6
2
В первом примере дерево выглядит следующим образом:
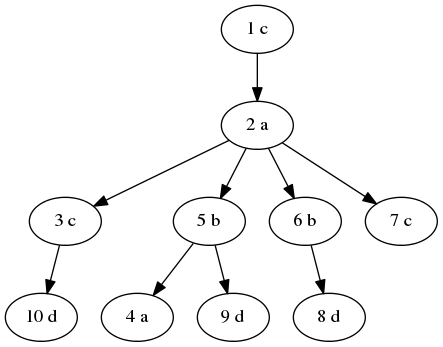
Наборы строк, которые могут быть прочитаны из вершин:
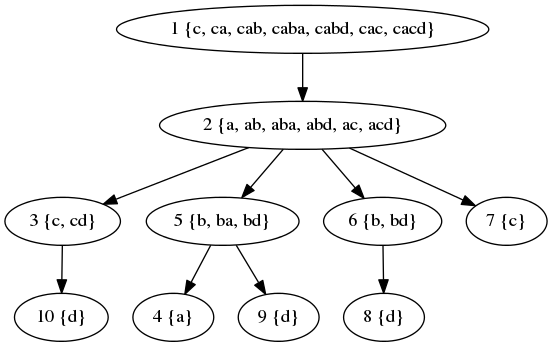
Наконец, значения 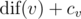 таковы:
таковы:
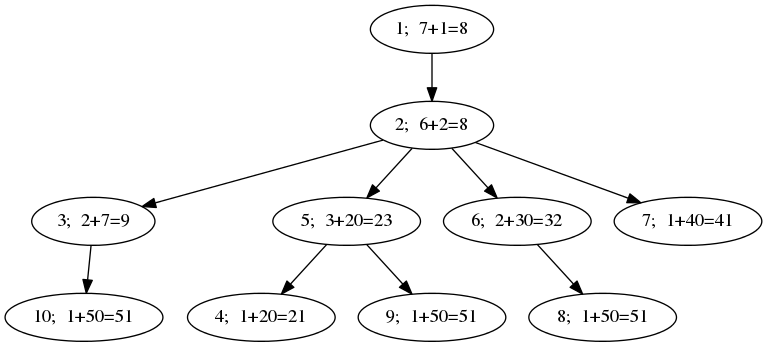
Во втором примере значения 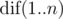 таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы:
таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы: 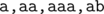 ; обратите внимание, что
; обратите внимание, что 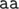 может быть прочитано как на пути до вершины 3, так и на пути до вершины 4.
может быть прочитано как на пути до вершины 3, так и на пути до вершины 4.
| Название |
|---|




