| Codeforces Round 332 (Div. 2) |
|---|
| Закончено |
Корневым деревом называется связный граф без циклов с выделенной вершиной. В рамках данной задачи будем считать, что корнем дерева всегда является вершина с номером 1.
Наименьшим общим предком вершин u и v называется наиболее удалённая от корня дерева вершина, лежащая как на пути от корня до u, так и на пути от корня до v. Будем обозначать наименьшего общего предка вершин u и v как LCA(u, v).
У белочки Сенди было корневое дерево, состоявшее из n вершин, в которых она хранила свои орешки. К несчастью, подводный шторм разрушил это дерево, и теперь Сенди никак не может его восстановить. Она смогла назвать m рёбер своего дерева и q троек чисел ai, bi и ci, про которые она полагает, что LCA(ai, bi) = ci.
Помогите Сенди посчитать, сколько существует деревьев с корнем в вершине 1, про которые верна вся информация, названная Сенди. Если же она что-то напутала, и таких деревьев не существует, то выведите 0. Два корневых дерева считаются различными, если существует хотя бы одно ребро, принадлежащее одному из этих деревьев и не принадлежащее другому.
В первой строке входных данных записаны три целых числа n, m и q (1 ≤ n ≤ 13, 0 ≤ m < n, 0 ≤ q ≤ 100) — количество вершин в дереве, а также количество рёбер и троек LCA, которые смогла вспомнить Сенди, соответственно.
Следующие m строк содержат по два целых числа ui и vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — номера вершин, соединённых i-м ребром. Гарантируется, что существует хотя бы одно дерево, такое что, удалив некоторые его рёбра, можно получить данные m рёбер.
Последние q строк содержат тройки чисел ai, bi, ci (1 ≤ ai, bi, ci ≤ n). Для каждой тройки Сенди полагает, что в исходном дереве было верно LCA(ai, bi) = ci. Существование дерева с данными значениями LCA не гарантируется.
Выведите количество деревьев размера n с корнем в вершине 1, таких что для них верна вся информация, которую помнит Сенди.
4 0 0
16
4 0 1
3 4 2
1
3 1 0
1 2
2
3 0 2
2 3 2
2 3 1
0
4 1 2
1 2
2 2 2
3 4 2
1
Во втором примере правильный ответ выглядит так:
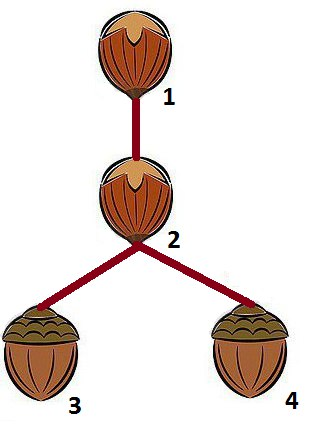
В третьем примере возможны два правильных ответа:

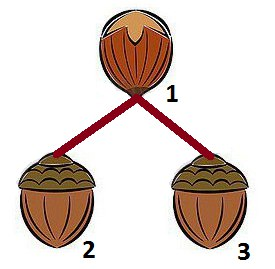
В четвёртом примере несложно заметить, что информация, предоставленная Сенди, противоречива.
| Название |
|---|




