| Codeforces Round 330 (Div. 1) |
|---|
| Закончено |
Сегодня на уроке математики Марья Ивановна рассказала Вовочке, что функция Эйлера целого положительного числа φ(n) — это мультипликативная арифметическая функция, равная количеству целых положительных чисел, меньших n и взаимно простых с ним. При этом полагают, что число 1 взаимно просто со всеми целыми положительными числами и что φ(1) = 1.
Теперь учительница дала Вовочке массив из n целых положительных чисел a1, a2, ..., an и задание обработать q запросов li ri — посчитать и вывести остаток от деления 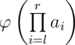 на 109 + 7. Поскольку это сложновато для второкласника, вы решили помочь Вовочке.
на 109 + 7. Поскольку это сложновато для второкласника, вы решили помочь Вовочке.
В первой строке входных данных записано число n (1 ≤ n ≤ 200 000) — длина массива, данного Вовочке. Во второй строке содержатся n чисел a1, a2, ..., an (1 ≤ ai ≤ 106).
В третьей строке содержится число q (1 ≤ q ≤ 200 000) — количество запросов. В следующих q строках по одному в каждой содержатся запросы. Каждый запрос определяется границами отрезка li и ri (1 ≤ li ≤ ri ≤ n).
Выведите q чисел — значение функции Эйлера для каждого из запросов, вычисленное по модулю 109 + 7.
10
1 2 3 4 5 6 7 8 9 10
7
1 1
3 8
5 6
4 8
8 10
7 9
7 10
1
4608
8
1536
192
144
1152
7
24 63 13 52 6 10 1
6
3 5
4 7
1 7
2 4
3 6
2 6
1248
768
12939264
11232
9984
539136
Во втором примере значения вычисляются так:
- φ(13·52·6) = φ(4056) = 1248
- φ(52·6·10·1) = φ(3120) = 768
- φ(24·63·13·52·6·10·1) = φ(61326720) = 12939264
- φ(63·13·52) = φ(42588) = 11232
- φ(13·52·6·10) = φ(40560) = 9984
- φ(63·13·52·6·10) = φ(2555280) = 539136
| Название |
|---|




