| Codeforces Round 330 (Div. 1) |
|---|
| Закончено |
У Эдо скопилась большая коллекция магнитиков на холодильник — целых n штук!
Он решил купить холодильник и повесить магнитики на его дверь. В магазине на заказ могут изготовить холодильник с любым размером двери, удовлетворяющим следующим ограничениям: дверь холодильника должна быть прямоугольником, а длина и ширина двери — целыми положительными числами.
Эдо придумал, как он хочет расположить магнитики на холодильнике. Он ввел систему координат на плоскости, представил каждый магнит в виде прямоугольника со сторонами, параллельными осям координат, и нарисовал их желаемое расположение.
Теперь он хочет убрать не более k магнитиков (возможно, не убирать ни одного) таким образом, чтобы все магнитики оказались прикреплены к двери холодильника, при этом площадь этой двери должна быть минимально возможной. Магнитик считается прикреплённым к двери холодильника, если его центр лежит на двери или на её границе. Относительное расположение неубранных магнитиков на двери холодильника должно совпадать с заданным на плане.
Поясним последние два предложения. Пусть мы хотим повесить на холодильник два магнита. Пусть магнит задан на плане координатами левого нижнего (x1, y1) и правого верхнего (x2, y2) углов, тогда его центр имеет координаты (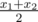
, 
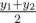) (возможно, не целые). Под сохранением относительного положения имеется в виду, что доступна только операция параллельного переноса всех магнитов, то есть вектор, соединяющий центры двух магнитов на изначальном плане, должен быть равен вектору, соединяющему центры этих двух магнитов при их расположении на холодильнике.
Стороны двери холодильника так же должны быть параллельны осям координат.
В первой строке содержатся два n и k (1 ≤ n ≤ 100 000, 0 ≤ k ≤ min(10, n - 1)) — количество магнитиков, имеющихся у Эдо, и максимальное количество магнитиков, которые можно не вешать на холодильник, соответственно.
Следующие n строк описывают план расположения магнитиков, нарисованный Эдо. В каждой строке содержится четыре целых числа x1, y1, x2, y2 (1 ≤ x1 < x2 ≤ 109, 1 ≤ y1 < y2 ≤ 109) — координаты левого нижнего и правого верхнего углов текущего магнитика соответственно. Магнитики могут как накладываться друг на друга частично, так и совпадать полностью.
Выведите единственное целое число — минимальную площадь двери холодильника, на которую можно повесить хотя бы n - k магнитиков, сохраняя относительный порядок.
3 1
1 1 2 2
2 2 3 3
3 3 4 4
1
4 1
1 1 2 2
1 9 2 10
9 9 10 10
9 1 10 2
64
3 0
1 1 2 2
1 1 1000000000 1000000000
1 3 8 12
249999999000000001
В первом тестовом примере оптимально удалить либо первый, либо третий магнитик. Если удалить первый магнитик, центры двух других будут лежать в точках (2.5, 2.5) и (3.5, 3.5). Таким образом, достаточно купить холодильник с шириной двери 1 и высотой двери 1, и, соответственно, площадью двери также равной 1.
Во втором тестовом примере неважно, какой из магнитиков удалить, потому что ответ все равно не изменится — нужен холодильник с шириной двери 8 и длиной двери 8.
В третьем тестовом примере ничего удалить нельзя, так как k = 0.
