| Codeforces Round 323 (Div. 1) |
|---|
| Закончено |
Дан бесконечный периодический массив a0, a1, ..., an - 1, ... с периодом длины n. Формально, 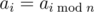 . Периодическим подмассивом (l, s) (0 ≤ l < n, 1 ≤ s < n) массива a называется бесконечный периодический массив с периодом длины s, период которого является подотрезком массива a, начинающегося с позиции l.
. Периодическим подмассивом (l, s) (0 ≤ l < n, 1 ≤ s < n) массива a называется бесконечный периодический массив с периодом длины s, период которого является подотрезком массива a, начинающегося с позиции l.
Периодический подмассив (l, s) называется превосходящим, если при совмещении его с массивом a, начиная с индекса l, любой элемент подмассива оказывается большим либо равным соответствующего ему в совмещении элемента массива a. Пример совмещения представлен на рисунке (сверху — бесконечный массив a, снизу — его периодический подмассив (l, s)):
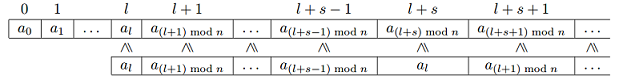
Найдите количество различных пар (l, s), соответствующих превосходящим периодическим подмассивам.
В первой строке содержится число n (1 ≤ n ≤ 2·105). Во второй строке содержатся n чисел a0, a1, ..., an - 1 (1 ≤ ai ≤ 106), разделенных пробелом.
Выведите единственное число — искомое количество пар.
4
7 1 2 3
2
2
2 1
1
3
1 1 1
6
В первом примере превосходящими являются подмассивы (0, 1) и (3, 2).
Подмассив (0, 1) является превосходящим, так как a0 ≥ a0, a0 ≥ a1, a0 ≥ a2, a0 ≥ a3, a0 ≥ a0, ...
Подмассив (3, 2) является превосходящим, так как a3 ≥ a3, a0 ≥ a0, a3 ≥ a1, a0 ≥ a2, a3 ≥ a3, ...
В третьем примере любая пара (l, s) соответствует превосходящему подмассиву, так как все элементы массива равны.
| Название |
|---|




