| Bubble Cup 8 - Finals [Online Mirror] |
|---|
| Закончено |
Саша и Ира — лучшие друзья. Они не просто друзья — они разработчики ПО и эксперты по искусственному интеллекту. Они разрабатывают алгоритм для двух ботов, играющих в игру для двух игроков. За каждый ход, один из игроков совершает ход (неважно, какой игрок, возможно, игроки делают ходы не по очереди).
Алгоритм для ботов, разработанный Сашей и Ирой, работает за счет отслеживания состояния, в котором находится игра. Каждый раз, когда любой бот делает ход, состояние меняется. А так как игра очень динамичная, она никогда не вернется в то состояние, в котором она была на каком-либо этапе в прошлом.
Саша и Ира — перфекционисты и они хотят, чтобы у их алгоритма была оптимальная выигрышная стратегия. Они заметили, что в оптимальной выигрышной стратегии оба бота делают ровно по N ходов каждый. Но для того, чтобы найти оптимальную стратегию, их алгоритму надо проанализировать все возможные состояния этой игры (они ещё не изучили альфа-бета отсечение) и выбрать лучшую последовательность ходов.
Они беспокоятся насчет эффективности их алгоритма и им интересно, какое общее количество состояний в игре, которое необходимо проанализировать?
В первой и единственной строке записано целое число N.
- 1 ≤ N ≤ 106
Вывод должен содержать единственное целое число – количество возможных состояний по модулю 109 + 7.
2
19
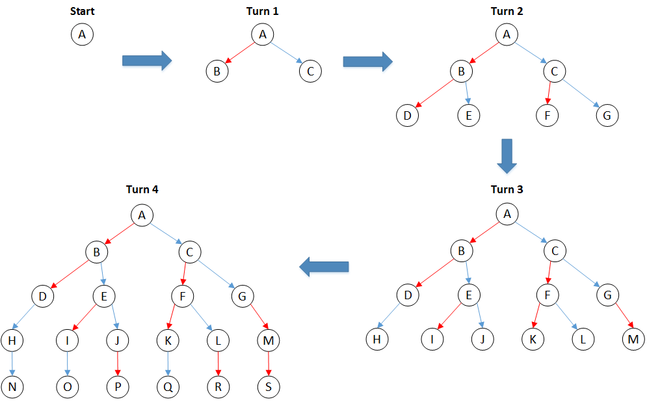
Начало: Игра в состоянии A.
- Ход 1: Любой бот может ходить (первый бот красный, а второй бот синий), так что есть два возможных состояния после первого хода – B и C.
- Ход 2: В обоих состояниях, B и C, любой бот может снова сделать ход, так что список возможных состояний расширяется и включает в себя D, E, F и G.
- Ход 3: Красный бот уже совершил N=2 движений в состоянии D, так что отсюда он больше не может делать ходов. Он может совершать ходы в состояниях E, F и G, так что состояния I, K и M добавляются в список. Аналогичным образом, синий бот не может совершать ходы в состоянии G, но может в D, E и F, так что добавляются состояния H, J и L.
- Ход 4: Красный бот точка уже совершил N=2 шага в состояниях H, I и K, он может двигаться только в J, L и M, так что добавляются состояния P, R и S. Синий бот не может двигаться в состояниях J, L и M, а только в H, I и K, так что добавляются состояния N, O и Q.
Всего образуется 19 различных состояний игры, необходимых в анализе алгоритма.
| Название |
|---|




