A. Фибоноччи
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Последовательность Фибоноччи — это целочисленная рекуррентная последовательность, определяемая следующим образом:

Fn = sn - 1·Fn - 1 + sn - 2·Fn - 2
при этом
F0 = 0, F1 = 1

Последовательность s — это бесконечная и почти периодическая последовательность с периодом длины N. Здесь последовательность s называется почти периодической с периодом длины N, если , для i ≥ N, кроме конечного числа значений si, для которых 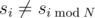(i ≥ N).

Далее следует пример почти периодической последовательности с периодом длины 4:

s = (5,3,8,11,5,3,7,11,5,3,8,11,…)

Обратите внимание, что единственное значение s, для которого не выполняется уравнение 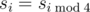— это s6 (s6 = 7 и s2 = 8). Вам даны s0, s1, ...sN - 1 и все значения последовательности s, для которых 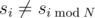(i ≥ N).

Найдите .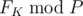

Входные данные

Первая строка содержит два целых числа, K и P. Во второй строке записано единственное число N. В третьей строке записано N чисел через пробелы, обозначающие первые N чисел последовательности s. В четвёртой строке записано единственное целое число M, количество значений в последовательности s, для которых 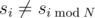. Каждая из последующих M строк содержит по два числа, j и v, обозначающих, что 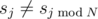и sj = v. Все значения j различны.

  • 1 ≤ N, M ≤ 50000
  • 0 ≤ K ≤ 1018
  • 1 ≤ P ≤ 109
  • 1 ≤ si ≤ 109, for all i = 0, 1, ...N - 1
  • N ≤ j ≤ 1018
  • 1 ≤ v ≤ 109
  • Все значения целочисленные.
Выходные данные

Выведите единственное целое число, равное .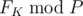

Примеры
Входные данные
10 8
3
1 2 1
2
7 3
5 4
Выходные данные
4