| Codeforces Round 313 (Div. 1) |
|---|
| Закончено |
Геральду надоело играть в настольные игры с обычным шестигранным кубиком и он купил себе игрушку, которая называется Рандомизатор. Он устроена следующим образом.
У Рандомизатора есть своя собственная координатная плоскость, на которой нарисован строго выпуклый многоугольник, называющийся основным многоугольником. Если Рандомизатор потрясти, он рисует некоторый невырожденный (т. е. имеющий ненулевую площадь) выпуклый многоугольник с вершинами в каких-то вершинах основного многоугольника. Результатом броска (точнее говоря, результатом потряхивания) считается количество точек с целыми координатами, которые оказались строго внутри (точки на границе не считаются) выбранного многоугольника. Теперь Геральду интересно — каково математические ожидание результата потряхивания Рандомизатора?
Во время потряхивания Рандомизатор рассматривает все возможные невырожденные выпуклые многоугольники с вершинами в вершинах основного многоугольника. Пусть оказалось k вариантов многоугольников. Тогда Рандомизатор выбирает каждый из них с вероятностью  .
.
В первой строке входных данных задано единственное число n (3 ≤ n ≤ 100 000) — количество вершин основного многоугольника.
В следующих n строках заданы координаты вершины основного многоугольника. В i-й из этих строк заданы два целых числа xi и yi ( - 109 ≤ xi, yi ≤ 109) — координаты i-й вершины многоугольника. Вершины даны в порядке обхода против часовой стрелки.
Выведите искомое математическое ожидание с абсолютной или относительной погрешностью не более 10 - 9.
4
0 0
2 0
2 2
0 2
0.2
5
0 0
2 0
2 2
1 3
0 2
0.8125
Многоугольник называется строго выпуклым, если он выпуклый, и никакие три его вершины не лежат на одной прямой.
Пусть случайная величина принимает значения x1, ..., xn с вероятностями p1, ..., pn соответственно. Тогда математическое ожидание этой случайной величины равняется 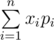 .
.
| Название |
|---|




