| Codeforces Round 311 (Div. 2) |
|---|
| Закончено |
После того, как Виталий был отчислен из университета, он увлекся теорией графов.
Особенно Виталию нравились циклы нечетной длины, в которых каждая вершина встречается не более одного раза.
Виталию стало интересно, как решать следующую задачу. Задан неориентированный граф из n вершин и m ребер, необязательно связный, без кратных ребер и петель. Нужно найти t — минимальное количество ребер, которые нужно добавить в заданный граф таким образом, чтобы образовался простой цикл нечетной длины, состоящий из более чем одной вершины. Кроме того, ему надо найти w — количество способов добавить t ребер так, чтобы образовался цикл нечетной длины (состоящий из более чем одной вершины). Запрещается добавлять петли или кратные рёбра.
Два способа добавить ребра в граф считаются одинаковыми, если в них совпадают множества добавляемых рёбер.
Так как Виталий уже не учится в университете, он обратился к вам за помощью в решении этой задачи.
В первой строке входных данных следуют два целых числа n и m (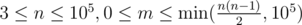 — количество вершин в графе и количество ребер в графе.
— количество вершин в графе и количество ребер в графе.
Следующие m строк содержат описания ребер графа, по одному ребру в строке. Каждое из ребер задается парой целых чисел ai, bi (1 ≤ ai, bi ≤ n) — номерами вершин, которые соединены i-м ребром. Все числа в строках разделены одним пробелом.
Гарантируется, что заданный граф не содержит петель и кратных ребер. Граф не обязательно является связным.
Выведите в первую строку выходных данных через пробел два целых числа t и w — минимальное количество ребер, которое необходимо добавить в граф, чтобы образовался простой цикл нечетной длины, состоящий из более чем одной вершины, в котором каждая вершина встречается не более одного раза, и количество способов сделать это.
4 4
1 2
1 3
4 2
4 3
1 2
3 3
1 2
2 3
3 1
0 1
3 0
3 1
Простой цикл это цикл, не проходящий дважды ни по какой вершине.
| Название |
|---|




