| Codeforces Round 309 (Div. 1) |
|---|
| Закончено |
Организация Nudist Beach (NB) планирует военную операцию по атаке организации Life Fibers (LF). Во время операции предполагается атаковать и захватить несколько городов, которые на настоящий момент находятся под контролем LF.
Дано n городов, обозначенных от 1 до n, и m двунаправленных дорог между ними. На данный момент в каждом из n городов установлена власть LF. Также в k из этих городов расположены крепости LF, и эти города нельзя захватить ни при каких обстоятельствах. Таким образом, NB может захватить произвольное непустое подмножество городов, не содержащих крепостей LF.
После операции NB придется защищать захваченные города от контратаки. Если они захватят город, соединенный со многими городами, контролируемыми LF, то их врагам будет легко отбить город обратно. Таким образом, NB хотят захватить множество городов, такое, что для каждого захваченного города отношение количества соседей, контролируемых NB, к количеству всех соседей этого города, было как можно больше.
Более формально, NB хотят захватить непустое множество городов S, не имеющих крепостей LF. Сила города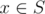 
определяется как (количество соседей x в S) / (общее количество соседей x), где соседними называются два города, соединённых дорогой. Цель NB — максимизировать силу самого слабого города в S.
Вам дано описание графа и городов с крепостями, найдите непустое подмножество, которое максимизирует силу самого слабого города.
В первой строке ввода находятся три целых числа n, m, k (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000, 1 ≤ k ≤ n - 1).
Во второй строке ввода находятся k целых чисел, представляющих города с крепостями. Все эти города различны.
В следующих m строках описаны дороги. В i-й из этих строк находятся 2 целых числа ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi). Гарантируется, что от каждого города отходит как минимум одна дорога.
Между каждой парой городов существует не более одной дороги.
В первой строке выведите целое число r, обозначающее размер оптимального множества (1 ≤ r ≤ n - k).
Во второй строке выведите r целых чисел, обозначающих города из оптимального множества. Города могут следовать в произвольном порядке. Эта строка не должна содержать ни одного города с крепостью.
Если существует несколько возможных ответов, выведите любой из них.
9 8 4
3 9 6 8
1 2
1 3
1 4
1 5
2 6
2 7
2 8
2 9
3
1 4 5
10 8 2
2 9
1 3
2 9
4 5
5 6
6 7
7 8
8 10
10 4
8
1 5 4 8 10 6 3 7
В первом примере достигается значение силы 1/2. Ни одно другое подмножество не даёт строго лучшего ответа.
Во втором примере достигается значение силы 1. Обратите внимание, что подмножество не обязательно должно быть связно.
