Вова и Марина любят предлагать друг другу головоломки. Сегодня Марина предложила Вове справиться со следующим заданием.
У Вовы есть неориентированный граф из n вершин и m рёбер, в котором нет петель и кратных рёбер. Определим операцию склейки двух не соединённых ребром вершин a и b. В результате этой операции вершины a и b стираются, а вместо них в граф добавляется новая вершина x, и из неё проводятся рёбра во все вершины, которые были соединены с a или с b (в частности, если вершина была соединена и с a, и с b, то также добавляется ровно одно ребро из x в неё). Таким образом, в результате склейки вновь образуется неориентированный граф без петель и кратных рёбер, но содержащий уже (n - 1) вершин.
Вова должен, выполнив склейку произвольное количество раз, преобразовать имеющийся граф в цепочку максимальной длины. Цепочкой длины k (k ≥ 0) называется связный граф, вершины которого можно пронумеровать числами от 1 до k + 1 таким образом, что рёбра графа будут соединять все пары вершин (i, i + 1) (1 ≤ i ≤ k) и только их. В частности, граф, состоящий из одной вершины, представляет собой цепочку длины 0. Вершины, образованные в результате склейки разрешается использовать в дальнейших операциях склейки.
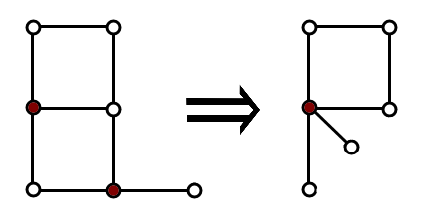 Рисунок иллюстрирует склейку двух вершин, помеченных красным цветом.
Рисунок иллюстрирует склейку двух вершин, помеченных красным цветом. Помогите Вове справиться с заданием его подруги. Найдите максимальную длину цепочки, которую можно получить из имеющегося графа, либо определите, что получить цепочку невозможно.
В первой строке находятся два целых числа n, m (1 ≤ n ≤ 1000, 0 ≤ m ≤ 100 000) — количество вершин и количество рёбер в исходном графе.
В следующих m строках находятся описания рёбер в формате ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi), что значит, что между вершинам ai и bi есть ребро. Гарантируется, что между каждой парой вершин есть не более одного ребра.
Если из данного графа невозможно получить цепочку, выведите - 1. В противном случае выведите максимальное возможное количество рёбер в полученной цепочке.
5 4
1 2
2 3
3 4
3 5
3
4 6
1 2
2 3
1 3
3 4
2 4
1 4
-1
4 2
1 3
2 4
2
В первом тесте из условия можно произвести склейку вершин 4 и 5 и получить цепочку длины 3.
Во втором тесте из условия исходно невозможно склеить никакую пару вершин, поэтому достигнуть требуемого невозможно.
В третьем тесте из условия можно склеить вершины 1 и 2 и получить цепочку длины 2.
| Название |
|---|




