| Codeforces Round 295 (Div. 2) |
|---|
| Закончено |
Вася увлекся биоинформатикой. Он собирается написать статью про похожие циклические последовательности ДНК, и поэтому он придумал новый способ определения схожести циклических последовательностей.
Пусть строки s и t имеют одинаковую длину n, тогда функция h(s, t) определяется как количество позиций, в которых соответствующие символы s и t совпадают. При помощи функции h(s, t), определяется функция расстояния по Василию ρ(s, t):
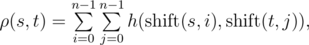
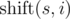 — это строка s, циклически сдвинутая на i символов влево. Например,
— это строка s, циклически сдвинутая на i символов влево. Например, Вася нашел в интернете строку s длины n. Теперь он хочет посчитать количество строк t, находящихся на максимальном расстоянии по Василию от строки s. Формально говоря, t должна удовлетворять равенству: 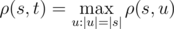 .
.
Вася не смог перебрать все возможные строки для нахождения ответа, поэтому ему нужна ваша помощь. Поскольку ответ может быть очень большим, посчитайте количество подходящих строк по модулю 109 + 7.
В первой строке ввода записано одно целое число n (1 ≤ n ≤ 105).
Во второй строке ввода записана одна строка длины n, состоящая из символов "ACGT".
Выведите одно число — ответ по модулю 109 + 7.
1
C
1
2
AG
4
3
TTT
1
Обратите внимание, что если для двух различных строк t1 и t2 значения ρ(s, t1) и ρ(s, t2) являются максимальными среди всех возможных строк, то обе строки необходимо учесть в итоговом количестве даже в том случае, когда одну из них можно получить циклическим сдвигом из другой.
В первом примере существует ρ("C", "C") = 1, для остальных строк t длины 1 значение ρ(s, t) равно 0.
Во втором примере ρ("AG", "AG") = ρ("AG", "GA") = ρ("AG", "AA") = ρ("AG", "GG") = 4.
В третьем примере ρ("TTT", "TTT") = 27.
| Название |
|---|




