| Rockethon 2015 |
|---|
| Закончено |
Вам дана перестановка из n чисел p1, p2, ..., pn. Мы совершаем k операций следующего типа: выбираем равновероятно случайным образом два индекса l и r (l ≤ r) и меняем порядок элементов pl, pl + 1, ..., pr на обратный. Ваша задача — определить математическое ожидание количества инверсий в итоговой перестановке.
Первая строка входных данных содержит два целых числа n и k (1 ≤ n ≤ 100, 1 ≤ k ≤ 109). Следующая строка содержит n целых чисел p1, p2, ..., pn — данную перестановку. Все pi различны и находятся в интервале от 1 до n.
Задача состоит из трех подзадач, которые отличаются друг от друга ограничениями на входные данные. За решение каждой подзадачи вы получите определенное количество баллов. Описание подзадач следует ниже.
- В подзадаче G1 (3 балла) выполняется 1 ≤ n ≤ 6, 1 ≤ k ≤ 4.
- В подзадаче G2 (5 баллов) выполняется 1 ≤ n ≤ 30, 1 ≤ k ≤ 200.
- В подзадаче G3 (16 баллов) выполняется 1 ≤ n ≤ 100, 1 ≤ k ≤ 109.
Выведите ответ на задачу с абсолютной или относительной погрешностью не более чем 1e - 9.
3 1
1 2 3
0.833333333333333
3 4
1 3 2
1.458333333333334
Рассмотрим первый пример. В перестановке (1, 2, 3) (которая изначально не содержит инверсий) будет выбран один интервал и порядок его элементов будет изменен на обратный. С вероятностью  , интервал будет состоять из одного элемента и перестановка не изменится. С вероятностью
, интервал будет состоять из одного элемента и перестановка не изменится. С вероятностью  мы поменяем местами первые два элемента и получим перестановку (2, 1, 3) с одной инверсией. С такой же вероятностью мы можем выбрать интервал, состоящий из последних двух элементов, что приведет к перестановке (1, 3, 2), в которой тоже одна инверсия. Наконец, с вероятностью
мы поменяем местами первые два элемента и получим перестановку (2, 1, 3) с одной инверсией. С такой же вероятностью мы можем выбрать интервал, состоящий из последних двух элементов, что приведет к перестановке (1, 3, 2), в которой тоже одна инверсия. Наконец, с вероятностью  выбранный случайным образом интервал будет содержать все элементы, что приведет к перестановке (3, 2, 1) с тремя инверсиями. Таким образом, мат.ожидание количества инверсий равно
выбранный случайным образом интервал будет содержать все элементы, что приведет к перестановке (3, 2, 1) с тремя инверсиями. Таким образом, мат.ожидание количества инверсий равно 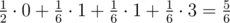 .
.
| Название |
|---|




