| Codeforces Round 287 (Div. 2) |
|---|
| Закончено |
Amr купил новую компьютерную игру "Угадай, где выход!". Цель игры— найти выход из лабиринта, похожего на полное двоичное дерево высоты h. Изначально игрок стоит в корне дерева, выход из дерева расположен в некотором листе дерева.
Пронумеруем все листы слева направо числами от 1 до 2h. Выход расположен в некоторой вершине n, где 1 ≤ n ≤ 2h.
Amr пользуется следующим простым алгоритмом выбора пути. Рассмотрим бесконечную строку "LRLRLRLRL..." (состоящую из чередующихся символов 'L' и 'R'). Amr последовательно выполняет символы строки по следующим правилам:
- Символ 'L' означает "перейти к левому сыну текущей вершины";
- Символ 'R' означает "перейти к правому сыну текущей вершины";
- Если вершину, в которую ведёт текущая команда, Amr уже это этого посещал, то он пропускает текущую команду, в противном случае он переходит в эту вершину;
- Если Amr пропустил две последовательные команды, то он возвращается к предку текущей вершины перед тем, как выполнять следующую команду;
- Если он оказался в листе, который не является выходом, он сразу возвращается к предку текущей вершины;
- Если он достиг выхода, игра заканчивается.
Теперь Amr интересно: если он будет следовать этому алгоритму, сколько вершин он посетит до того, как достичь выхода?
Ввод состоит из двух целых чисел, h, n (1 ≤ h ≤ 50, 1 ≤ n ≤ 2h).
Выведите единственное целое число, обозначающее количество вершин (не включая лист, в котором расположен выход), которые Amr посетит перед тем, как добраться до выхода, следуя этому алгоритму.
1 2
2
2 3
5
3 6
10
10 1024
2046
Полное двоичное дерево высоты h— это двоичное дерево, состоящее из h + 1 уровня. Уровень 0 состоит из единственной вершины, которая называется корень, уровень h состоит из 2h вершин, которые называются листьями. Каждая вершина, не являющаяся листом, имеет ровно двух потомков, левого и правого.
Следующая картина иллюстрирует третий тест из условия. Вершины помечены в порядке их посещения.
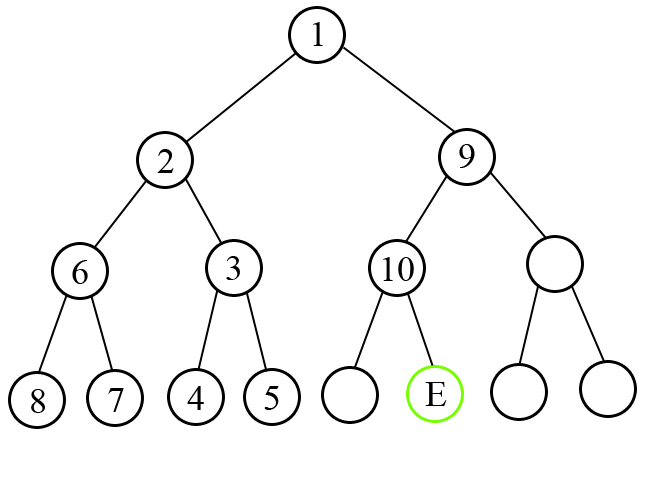
| Название |
|---|




