| Codeforces Round 286 (Div. 2) |
|---|
| Закончено |
Мистер Китаюта недавно приобрёл неориентированный граф, состоящий из n вершин и m ребер. Вершины графа пронумерованы от 1 до n. Ребро i окрашено в цвет ci и соединяет вершины ai и bi.
Мистер Китаюта хочет, чтобы вы обработали q запросов следующего вида.
В i-м запросе он дает вам два целых числа — ui и vi. Вам требуется найти количество цветов, таких, что ребра этого цвета непосредственно или косвенно соединяют вершины ui и vi (т. е. по рёбрам только этого цвета можно добраться от вершины ui до вершины vi).
В первой строке следуют два целых числа через пробел — n и m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), обозначающие количество вершин и количество ребер, соответственно.
В следующих m строках следуют три целых числа через пробел — ai, bi (1 ≤ ai < bi ≤ n) и ci (1 ≤ ci ≤ m). Обратите внимание, что между двумя вершинами может быть несколько ребер. Однако между двумя вершинами не может быть нескольких ребер одного цвета, таким образом, если i ≠ j, то (ai, bi, ci) ≠ (aj, bj, cj).
В следующей строке записано целое число — q (1 ≤ q ≤ 100), обозначающее количество запросов.
Затем следует q строк по два целых числа через пробел — ui и vi (1 ≤ ui, vi ≤ n). Гарантируется, что ui ≠ vi.
Для каждого запроса выведите ответ в отдельной строке.
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4
2
1
0
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4
1
1
1
1
2
Рассмотрим первый пример.
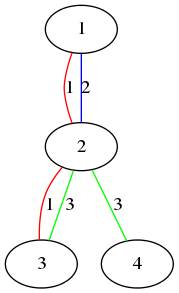Рисунок выше иллюстрирует первый пример. - Вершина 1 и вершина 2 соединены цветами 1 и 2.
- Вершина 3 и вершина 4 соединены цветом 3.
- Вершина 1 и вершина 4 не соединены никаким цветом.
