| Codeforces Round 278 (Div. 1) |
|---|
| Закончено |
В Киберленде n городов, пронумерованных от 1 до n и соединенных m двунаправленных дорогами. j-я дорога соединяет города aj и bj.
В каждом городе Киберленда продаются сувениры для туристов. В частности, город i продает сувениры по цене wi.
Вам надо обработать q запросов. Запросы бывают двух типов:
- "C a w": Цена в городе a меняется на w.
- "A a b": Турист едет из города a в город b. Для этого он выбирает путь, при этом, турист не хочет посетить никакой город дважды. Он собирается купить сувениры в том городе, где сувениры самые дешевые (возможно, прямо в городе a или b). Вам следует вывести наименьшую возможную цену, по которой он может купить сувениры, путешествуя по некоторому простому пути.
- Путь — это последовательность городов [x1, x2, ..., xk], где k — некоторое положительное число.
- Для любых 1 ≤ i < j ≤ k, xi ≠ xj.
- Для любого 1 ≤ i < k есть дорога, соединяющая xi и xi + 1.
- Наименьшая стоимость на пути равна min(wx1, wx2, ..., wxk).
- Искомый ответ — это наименьшее значение наименьших стоимостей на всех корректных путях из a в b.
В первой строке входного файла записано три разделённых пробелами целых числа n, m, q (1 ≤ n, m, q ≤ 105).
В следующих n строках записаны целые числа wi (1 ≤ wi ≤ 109).
В следующих m строках записано по два разделённых пробелами целых числа, aj и bj (1 ≤ aj, bj ≤ n, aj ≠ bj).
Одна и та же пара городов соединяется не более чем одной дорогой. Между любыми двумя городами всегда есть по крайней мере один корректный путь.
Далее следует q строк, в каждой из которых записано по запросу. Формат строки: "C a w" или "A a b" (1 ≤ a, b ≤ n, 1 ≤ w ≤ 109).
Для каждого запроса типа "A" выведите соответствующий ответ.
3 3 3
1
2
3
1 2
2 3
1 3
A 2 3
C 1 5
A 2 3
1
2
7 9 4
1
2
3
4
5
6
7
1 2
2 5
1 5
2 3
3 4
2 4
5 6
6 7
5 7
A 2 3
A 6 4
A 6 7
A 3 3
2
1
5
3
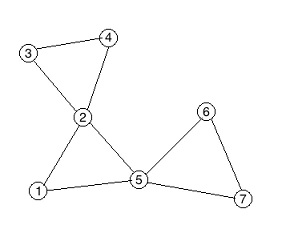
Во втором примере оптимальные пути таковы:
Из 2 в 3 — [2, 3].
Из 6 в 4 — [6, 5, 1, 2, 4].
Из 6 в 7 — [6, 5, 7].
Из 3 в 3 — [3].
| Название |
|---|




