| Codeforces Round 277 (Div. 2) |
|---|
| Закончено |
Как вы, наверное, знаете, неориентированный связный граф с n вершинами и n - 1 ребрами называется деревом. Вам дано целое число d и дерево, состоящее из n вершин. С каждой вершиной i связано её значение ai.
Назовем множество S вершин дерева допустимым, если выполняются следующие условия:
- S является непустым множеством.
- S является связным множеством. Иными словами, если вершины u и v содержатся во множестве S, то все вершины, лежащие на простом пути между u и v должны также лежать в S.
-
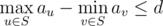 .
.
Ваша задача — посчитать количество допустимых множеств. Так как результат может быть очень большим, выведите его остаток по модулю 1000000007 (109 + 7).
В первой строке содержатся два целых числа через пробел, d (0 ≤ d ≤ 2000) и n (1 ≤ n ≤ 2000).
Во второй строке записано n целых положительных чисел, разделённых пробелами, a1, a2, ..., an(1 ≤ ai ≤ 2000).
В следующих n - 1 строках записано по паре целых чисел u и v (1 ≤ u, v ≤ n), обозначающих наличие ребра между u и v. Гарантируется, что данный граф является деревом.
Выведите количество допустимых множеств по модулю 1000000007.
1 4
2 1 3 2
1 2
1 3
3 4
8
0 3
1 2 3
1 2
2 3
3
4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4
41
В первом примере можно найти ровно 8 допустимых множеств: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} и {1, 3, 4}. Множество {1, 2, 3, 4} не является допустимым, поскольку оно не отвечает третьему условию. Множество {1, 4} отвечает третьему условию, но противоречит второму условию.
| Название |
|---|




