| Codeforces Round 269 (Div. 2) |
|---|
| Закончено |
Белые медведи Меньшиков и Услада из Санкт-Петербургского зоопарка и слоник Хорас из Киевского зоопарка решили построить карточный домик. Для этого они уже нашли внушительную колоду, содержащую n игральных карт. Давайте опишем домик, который они хотят собрать:
- Домик состоит из некоторого ненулевого количества этажей.
- Каждый этаж состоит из ненулевого количества комнат и потолка. Комната — две карты, прислоненных друг к другу. Комнаты располагаются в ряд, и на каждые две соседние комнаты кладется потолок из еще одной карты.
- Каждый этаж, кроме самого нижнего, должен содержать меньше комнат, чем этаж ниже.
Обратите внимание, что домик может заканчиваться этажом с более чем одной комнатой и в таком случае их тоже требуется накрыть потолком. Также количество комнат на соседних этажах не обязательно должно отличаться на единицу, разница может быть больше.
Пока медведи тренируются ставить карты, Хорас пытается сообразить, из скольки этажей должен состоять их дом. Назовем высотой дома количество этажей в нем. Возможно, что из n карт можно собрать много разных домиков разных высот. Кажется, эта задача слонику не под силу, он просит вас посчитать, домики скольки различных высот они смогут собрать, использовав ровно n карт.
В единственной строке находится целое число n (1 ≤ n ≤ 1012) — количество карт.
Выведите количество различных высот, которые могут быть у домиков, построенных ровно из n карт.
13
1
6
0
В первом примере, использовав все 13 карт, можно построить только такие два дома:
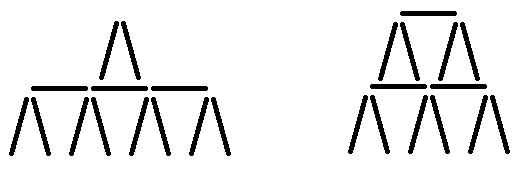
Таким образом из 13 карт можно построить только двухэтажные домики, поэтому ответ — 1.
Из шести карт во втором примере ни одного домика построить нельзя.
| Название |
|---|




