| Codeforces Round 259 (Div. 1) |
|---|
| Закончено |
Однажды Twilight Sparkle играла в Ludo со своими друзьями: Rainbow Dash, Apple Jack и Flutter Shy. К сожалению, она все время проигрывала. Вернувшись в замок, Twilight Sparkle решила изучить игральные кости, которые использовались в игре.
Игральная кость, которая использовалась в игре, имеет m граней: на первой грани игральной кости нарисована одна точка, на второй грани нарисовано две точки и так далее, на m-й грани нарисовано m точек. Twilight Sparkle точно знает, что при броске кости каждая грань выпадает с вероятностью 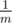 . Также она уверена, что каждый бросок независим от других. Помогите ей посчитать математическое ожидание максимального количества точек на грани среди n бросков игральной кости.
. Также она уверена, что каждый бросок независим от других. Помогите ей посчитать математическое ожидание максимального количества точек на грани среди n бросков игральной кости.
Единственная строка содержит два целых числа, m и n (1 ≤ m, n ≤ 105).
Выведите единственное вещественное число — математическое ожидание максимума. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превысит 10 - 4.
6 1
3.500000000000
6 3
4.958333333333
2 2
1.750000000000
Рассмотрим третий тестовый пример. Выполнив два броска, можно получить:
- В первом броске 1, во втором броске 2. Максимум в этом случае равен 2.
- В первом броске 1, во втором броске 1. Максимум в этом случае равен 1.
- В первом броске 2, во втором броске 1. Максимум в этом случае равен 2.
- В первом броске 2, во втором броске 2. Максимум в этом случае равен 2.
Вероятность каждого из исходов 0.25, поэтому математическое ожидание максимума равно:
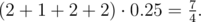
Про математическое ожидание можно почитать по ссылке: http://ru.wikipedia.org/wiki/Математическое_ожидание
| Название |
|---|




