| Codeforces Round 254 (Div. 1) |
|---|
| Закончено |
DZY любит садоводство, поэтому он обожает решать задачи про деревья.
У DZY есть взвешенное дерево (связный неориентированный граф без циклов), состоящее из n вершин (пронумерованных от 1 до n). Определим функцию g(x, y) (1 ≤ x, y ≤ n) как длину самого длинного ребра в кратчайшем пути между вершинами x и y. В частности, g(z, z) = 0 для любого z.
Для каждой целочисленной последовательности p1, p2, ..., pn (1 ≤ pi ≤ n), определим f(p) как 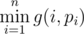 .
.
DZY хочет найти такую последовательность p, что f(p) принимает максимальное возможное значение. Есть еще одно ограничение: элемент j может встречаться в p не более xj раз.
Пожалуйста, помогите DZY, найдите максимальное возможное f(p) при описанных ограничениях.
В первой строке записано целое число n (1 ≤ n ≤ 3000).
В каждой из следующих n - 1 строк записано по три целых числа ai, bi, ci (1 ≤ ai, bi ≤ n; 1 ≤ ci ≤ 10000), обозначающих ребро между вершинами ai и bi длины ci. Гарантируется, что эти ребра образуют дерево.
Каждая из следующих n строк описывает элемент последовательности x. В j-й строке записано целое число xj (1 ≤ xj ≤ n).
Выведите единственное целое число — ответ на задачу.
4
1 2 1
2 3 2
3 4 3
1
1
1
1
2
4
1 2 1
2 3 2
3 4 3
4
4
4
4
3
В первом примере одна из оптимальных последовательностей p равна [4, 3, 2, 1].
| Название |
|---|




