| Codeforces Round 242 (Div. 2) |
|---|
| Закончено |
Недавно состоялось официальное заявление мирового олимпийского комитета, согласно которому зимние Олимпийские игры 2030 года пройдут в Томске. Городские власти решили основательно подготовиться к проведению олимпиады и как можно раньше построить все необходимые олимпийские объекты. Первой построена будет биатлонная трасса.
Для строительства биатлонной трассы был выделен участок земли, представляющий собой прямоугольник, разбитый на n × m одинаковых квадратов. Каждый квадрат имеет координаты: номер строки (от 1 до n), в которой он находится, и номер столбца (от 1 до m), в котором он находится. Более того, каждый из квадратов характеризуется своей высотой. В ходе спортивных состязаний биатлонисты будут вынуждены передвигаться из одного квадрата в другой. Если перемещение происходит из более высокого квадрата в более низкий, то биатлонист совершает спуск. Если биатлонист перемещается из более низкого квадрата в более высокий, то он совершает подъем. Если биатлонист перемещается между двумя квадратами с одинаковой высотой, то он двигается по ровной местности.
Биатлонная трасса должна представлять собой границу некоторой прямоугольной области выделенного земельного участка, по которой биатлонисты будут двигаться в направлении движения по часовой стрелке. Известно, что на одно перемещение по ровной местности среднестатистический биатлонист тратит tp секунд, на один подъем — tu секунд, на один спуск — td секунд. Томская администрация хочет выбрать трассу таким образом, чтобы время ее прохождения среднестатистическим биатлонистом было как можно ближе к t секундам. Другими словами, разность времени ts прохождения выбранной трассы и t должна быть минимальна.
Для более четкого понимания можно рассмотреть первый пример входных данных. В этом примере n = 6, m = 7, а администрация хочет, чтобы время прохождения трассы было как можно ближе к t = 48 секундам, причем tp = 3, tu = 6 и td = 2. Если рассмотреть показанный стрелками на изображении прямоугольник, то при движении по его границе по часовой стрелке у среднестатистического биатлониста уйдет ровно 48 секунд. Левый верхний угол этой трассы расположен в квадрате с номером строки 4 и номером столбца 3, а правый нижний — в квадрате с номером строки 6 и номером столбца 7.
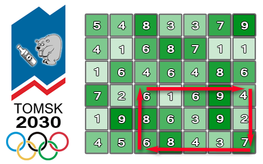
Администрация, помимо всего прочего, хочет, чтобы все стороны прямоугольника, по границе которого будут двигаться биатлонисты, состояли не менее чем из трех квадратов и полностью размещалась внутри выделенного земельного участка.
Вас привлекли для написания программы, которая для заданного земельного участка и всех необходимых временных величин найдет наиболее подходящий прямоугольник для создания биатлонной трассы. Если таких прямоугольников несколько — разрешается вывести любой из них.
В первой строке входных данных содержатся три целых числа n, m и t (3 ≤ n, m ≤ 300, 1 ≤ t ≤ 109) — размеры земельного участка и желательное время прохождения.
Во второй строке так же содержатся три целых числа tp, tu и td (1 ≤ tp, tu, td ≤ 100) — время прохождения среднестатистическим биатлонистом ровного участка трассы, подъема и спуска соответственно.
Далее следует n строк по m целых чисел, задающих высоты каждого из квадратов выделенного земельного участка. Каждое из значений высот — целое положительное число, не превышающее 106.
В единственной строке выходных данных требуется вывести четыре целых положительных числа — номер строки и номер столбца левого верхнего угла, а также номер строки и номер столбца правого нижнего угла выбранного для трассы прямоугольника.
6 7 48
3 6 2
5 4 8 3 3 7 9
4 1 6 8 7 1 1
1 6 4 6 4 8 6
7 2 6 1 6 9 4
1 9 8 6 3 9 2
4 5 6 8 4 3 7
4 3 6 7
| Название |
|---|




