| Codeforces Round 238 (Div. 2) |
|---|
| Закончено |
Маленький Крис знает, что играть в домино неинтересно, он думает, что в игре слишком много случайного и совсем не требуется умение. Поэтому он решил поиграть с доминошками и устроить «домино шоу».
Крис расположил n доминошек в ряд, поставив каждую вертикально вверх. В начале он выбирает некоторые доминошки, и толкает каждую из них либо влево, либо вправо. Однако, между каждыми двумя доминошками, толкаемыми в одном направлении, обязательно находится хотя бы одна доминошка, которую Крис толкнул в противоположном направлении.
Через каждую секунду каждая доминошка, падающая влево, толкает соседнюю доминошку слева. Аналогично, доминошки, падающие вправо, толкают соседние доминошки справа. Когда на вертикальную доминошку падают соседние доминошки с обеих сторон, она не двигается из-за баланса сил слева и справа. Рисунок ниже показывает один из возможных примеров описанного процесса.
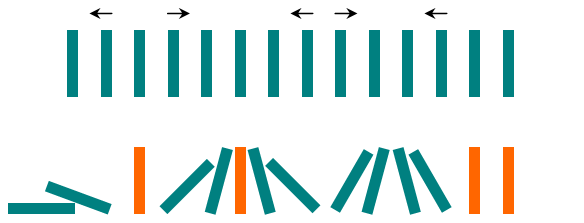
Вам даны изначальные направления, в которых Крис толкает доминошки. Найдите количество доминошек, которые останутся стоять вертикально в конце процесса!
В первой строке записано единственное целое число n (1 ≤ n ≤ 3000) — количество доминошек в ряду. В следующей строке записана строка s длины n. При этом, i-й символ строки si равняется:
- «L», если Крис изначально толкнул i-ю доминошку влево;
- «R», если Крис изначально толкнул i-ю доминошку вправо;
- «.», если Крис изначально не толкнул i-ю доминошку.
Гарантируется, что если si = sj = «L» и i < j, то существует такой индекс k, что i < k < j и sk = «R»; если si = sj = «R» и i < j, тогда существует такой индекс k, что i < k < j и sk = «L».
Выведите единственное целое число — количество доминошек, которые останутся в конце концов вертикальными.
14
.L.R...LR..L..
4
5
R....
0
1
.
1
Первый пример показан на рисунке. Четыре доминошки, оставшиеся стоять вертикально, выделены оранжевым цветом.
Во втором тестовом примере все доминошки падают, так как первая доминошка падает на все остальные.
В последнем примере, единственную доминошку не толкали ни в одном направлении.
| Название |
|---|




