| Codeforces Round 236 (Div. 2) |
|---|
| Закончено |
Будем называть неориентированный граф из n вершин p-интересным, если выполнены условия:
- граф содержит ровно 2n + p ребер;
- граф не содержит петель и кратных ребер;
- для любого целого k (1 ≤ k ≤ n) любой подграф, состоящий из k вершин, содержит не более 2k + p ребер.
Подграфом графа будем называть некоторое множество вершин графа и некоторое множество ребер графа. Причем множество ребер должно удовлетворять условию: оба конца каждого ребра из множества должны принадлежать выбранному множеству вершин.
Ваша задача отыскать p-интересный граф, состоящий из n вершин.
В первой строке задано единственное целое число t (1 ≤ t ≤ 5) — количество тестовых данных. В следующих t строках задано по два целых числа: n, p (5 ≤ n ≤ 24; p ≥ 0; 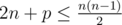 ) — количество вершин в графе и параметр интересности для соответствующего теста.
) — количество вершин в графе и параметр интересности для соответствующего теста.
Гарантируется, что искомый граф существует.
Для каждого из t тестов выведите 2n + p строк, содержащих описание ребер p-интересного графа: i-я строка должна содержать два целых числа через пробел ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — две вершины, соединенные ребром в результирующем графе. Считайте, что вершины графа пронумерованы целыми числами от 1 до n.
Ответы для тестов выводите в том порядке, в котором тесты заданы во входных данных. Если существует несколько решений, разрешается вывести любое из них.
1
6 0
1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6
| Название |
|---|




